��Ŀ����
6��4��ͬ�ͺŵIJ�Ʒ�У���1�����ϸ�Ʒ��3���ϸ�Ʒ����1������4����Ʒ�������ȡ1�����м�⣬��鵽���Dz��ϸ�Ʒ�ĸ��ʣ�
��2������4����Ʒ�������ȡ2�����м�⣬��鵽�Ķ��Ǻϸ�Ʒ�ĸ��ʣ�
��3������4����Ʒ�м���x���ϸ�Ʒ�����������飺�����ȡ1�����м�⣬Ȼ��Żأ�����ظ�������飬ͨ�������ظ�������֣��鵽�ϸ�Ʒ��Ƶ���ȶ���0.95������������x��ֵ��Լ�Ƕ��٣�
���� ��1���ò��ϸ�Ʒ��������������������ó鵽���ϸ�Ʒ�ĸ��ʣ�
��2�����ö����¼�ͬʱ�����ĸ��ʵ������������¼����������ĸ��ʵĻ����ɼ��㣻
��3������Ƶ�ʹ��Ƴ����ʣ����ø��ʹ�ʽ��ʽ���㼴�����x��ֵ��
��� �⣺��1����4��ͬ�ͺŵIJ�Ʒ�У���1�����ϸ�Ʒ��
��P�����ϸ�Ʒ��=$\frac{1}{4}$��
��2��
����12��������鵽�Ķ��Ǻϸ�Ʒ�������6�֣�
P���鵽�Ķ��Ǻϸ�Ʒ��=$\frac{6}{12}$=$\frac{1}{2}$��
��3���ߴ����ظ�������֣��鵽�ϸ�Ʒ��Ƶ���ȶ���0.95��
��鵽�ϸ�Ʒ�ĸ��ʵ���0.95��
��$\frac{x+3}{x+4}$=0.95��
��ã�x=16��
���� ���⿼���˸��ʵĹ�ʽ���б�������״ͼ������Ƶ�ʹ��Ƹ��ʵ�֪ʶ������Ĺؼ����˽�����ظ��������¼�������Ƶ�ʿ��Թ��Ƹ��ʣ�

��ϰ��ϵ�д�
 �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�
�����Ŀ
1����֪Բ�İ뾶��2$\sqrt{3}$�����Բ���ڽ��������ε�����ǣ�������
| A�� | 3$\sqrt{3}$ | B�� | 9$\sqrt{3}$ | C�� | 18$\sqrt{3}$ | D�� | 36$\sqrt{3}$ |
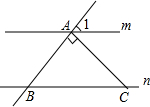 ��ͼ��ֱ��m��n����ABCΪ���������Σ���BAC=90�㣬���1=45�ȣ�
��ͼ��ֱ��m��n����ABCΪ���������Σ���BAC=90�㣬���1=45�ȣ�