题目内容
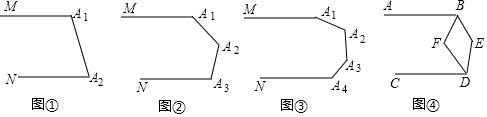
1．（1）如图①，MA1∥NA2，则∠A1+∠A2=180°；如图②，MA1∥NA3，则∠A1+∠A2+∠A3=360°，请你说明理由；
（2）如图③，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4=540°；
（3）利用上述结论解决问题：如图④，AB∥CD，∠ABE和∠CDE的平分线相交于点F，∠E=140°，求∠BFD的度数．
分析 （1）根据两直线平行，同旁内角互补即可得到结论；
（2）过A2作PA2∥MA1，过A3作QA3∥MA1，根据两直线平行，同旁内角互补即可得到∠A1+∠A2+∠A3+∠A4=540°；
（3）过F作FG∥AB，则AB∥CD∥FG，根据（1）中的结论以及角平分线的定义，即可得到∠BFD=$\frac{1}{2}$（∠ABE+∠CDE）=110°．
解答 解：（1）如图①，根据MA1∥NA2，可得∠A1+∠A2=180°，
如图②，过A2作PA2∥MA1，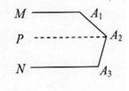
∵MA1∥NA3，
∴PA2∥MA1∥NA3，
∴∠A1+∠A1A2P=180°，∠A3+∠A3A2P=180°，
∴∠A1+∠A1A2A3+∠A3=360°；
故答案为：180°，360°；
（2）如图③，过A2作PA2∥MA1，过A3作QA3∥MA1，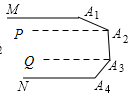
∵MA1∥NA3，
∴QA3∥PA2∥MA1∥NA3，
∴∠A1+∠A1A2P=180°，∠QA3A2+∠A3A2P=180°，∠A4+∠A4A3Q=180°，
∴∠A1+∠A2+∠A3+∠A4=540°；
故答案为：540°；
（3）如图④，过F作FG∥AB，则AB∥CD∥FG，
∴∠BFG=∠ABF，∠GFD=∠CDF，
∵∠ABE和∠CDE的平分线相交于点F，
∴∠BFD=$\frac{1}{2}$（∠ABE+∠CDE），
又∵∠ABE+∠E+∠CDE=360°，∠E=140°，
∴∠ABE+∠CDE=220°，
∴∠BFD=110°．
点评 本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补．解决问题的关键是作平行线，构造同旁内角．
练习册系列答案
快乐5加2金卷系列答案
相关题目
如果抛物线C1的顶点在抛物线C2上，同时，抛物线C2的顶点在抛物线C1上，那么，我们称抛物线C1与C2关联．
9．
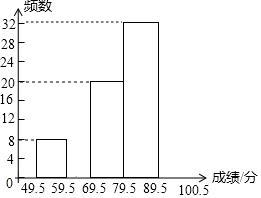6月5日是世界环境日，为了普及环保知识，增强环保意识，某市第一中学举行了“环保知识竞赛”，参赛人数1000人，为了了解本次竞赛的成绩情况，学校团委从中抽取部分学生的成绩（满分为100分，得分取整数）进行统计，并绘制出不完整的频数分布表和不完整的频数分布直方图如下：
（1）直接写出a的值，并补全频数分布表和频数分布直方图．
（2）若成绩在80分以上为优秀，求这次参赛的学生中成绩为优秀的约有多少人？
6月5日是世界环境日，为了普及环保知识，增强环保意识，某市第一中学举行了“环保知识竞赛”，参赛人数1000人，为了了解本次竞赛的成绩情况，学校团委从中抽取部分学生的成绩（满分为100分，得分取整数）进行统计，并绘制出不完整的频数分布表和不完整的频数分布直方图如下：| 分组 | 频数 | 所占百分比 |
| 49.5～59.5 | 8 | 8% |
| 59.5～69.5 | 12 | 12% |
| 69.5～79.5 | 20 | 20% |
| 79.5～89.5 | 32 | 32% |
| 89.5～100.5 | 28 | a |
（2）若成绩在80分以上为优秀，求这次参赛的学生中成绩为优秀的约有多少人？
如图，立方体棱长为2cm，将线段AC平移到A1C1的位置上，平移的距离是2cm．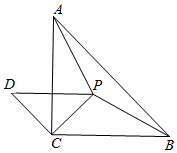
在等腰Rt△ABC中，∠ACB=90°，点P是△ABC内一点，且CP=$\sqrt{2}$，BP=AP=2，以点C为直角顶点，CP为直角边，作如图的等腰Rt△DCP，有如下4个结论：①点A与D的距离为2；②∠CPB=105°；③AB=$\sqrt{6}+\sqrt{2}$；④S△APB=2，其中正确的结论是（ ）
