题目内容
12.已知a-b=5,ab=2,求代数式a3b-2a2b2+ab3的值.分析 首先把代数式a3b-2a2b2+ab3分解因式,然后尽可能变为和a-b、ab相关的形式,然后代入已知数值即可求出结果.
解答 解:a3b-2a2b2+ab3=ab(a2-2ab+b2)=ab(a-b)2,
∵a-b=5,ab=2,
∴原式=2×52=50.
点评 此题主要考查了分解因式的应用,正确应用公式是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
17. 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③HD平分∠AHC,④△BCE≌△COD中,正确的有( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③HD平分∠AHC,④△BCE≌△COD中,正确的有( )
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③HD平分∠AHC,④△BCE≌△COD中,正确的有( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③HD平分∠AHC,④△BCE≌△COD中,正确的有( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
2.下列等式由左边到右边的变化,属于因式分解的是( )
| A. | x2+5x-1=x(x+5)-1 | B. | x2+3x-4=x(x+3-$\frac{4}{x}$) | C. | x2-9=(x+3)(x-3) | D. | (x+2)(x-2)=(x-2)(x+2) |

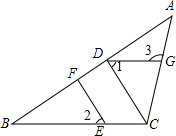 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.