题目内容
4.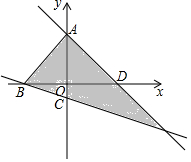 在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,-1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )
在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,-1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据勾股定理即可得出OB的长度,由此可得出点B的坐标,由OA、OD的长度可得出点A、D的坐标,根据点A、D、B、C的坐标利用待定系数法即可求出直线AD、BC的解析式,联立两直线解析式成方程组,通过解方程组即可求出其交点的坐标,再根据点(a,b)在如图所示的阴影部分内部(不包括边界)结合点B以及交点的横坐标即可得出结论.
解答 解:∵AB=5,OA=4,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=3,
∴点B(-3,0).
∵OA=OD=4,
∴点A(0,4),点D(4,0).
设直线AD的解析式为y=kx+b,
将A(0,4)、D(4,0)代入y=kx+b,
$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴直线AD的解析式为y=-x+4;
设直线BC的解析式为y=mx+n,
将B(-3,0)、C(0,-1)代入y=mx+n,
$\left\{\begin{array}{l}{-3m+n=0}\\{n=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=-1}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{1}{3}$x-1.
联立直线AD、BC的解析式成方程组,
$\left\{\begin{array}{l}{y=-x+4}\\{y=-\frac{1}{3}x-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{15}{2}}\\{y=-\frac{7}{2}}\end{array}\right.$,
∴直线AD、BC的交点坐标为($\frac{15}{2}$,-$\frac{7}{2}$).
∵点(a,b)在如图所示的阴影部分内部(不包括边界),
∴-3<a<$\frac{15}{2}$.
故选D.
点评 本题考查了两条直线相交或平行问题、在数轴上表示不等式的解集、待定系数法求一次函数解析式以及解二元一次方程组,根据点的坐标利用待定系数法求出一次函数解析式是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a+3>b+3 | B. | 2 a>2 b | C. | -a<-b | D. | a-b<0 |
| A. | 互余但不相等 | B. | 互为补角 | C. | 相等但不互余 | D. | 互余且相等 |
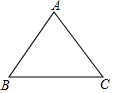 已知在三角形ABC中,AB=AC=5,BC=6,求三角形ABC的面积.
已知在三角形ABC中,AB=AC=5,BC=6,求三角形ABC的面积.
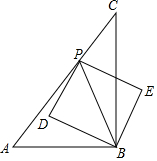 定义,若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”,如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA-AB以5cm/s的速度运动,当电P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
定义,若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”,如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA-AB以5cm/s的速度运动,当电P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).