题目内容
13.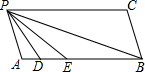 如图所示,已知PC∥AB,∠APC=∠ABC=80°,D、E在AB上,且满足∠BPC=∠BPE,∠APD=∠DPE.
如图所示,已知PC∥AB,∠APC=∠ABC=80°,D、E在AB上,且满足∠BPC=∠BPE,∠APD=∠DPE.(1)求∠BPD的度数;
(2)现将BC平行移动,试探究∠ABP:∠AEP的值是否发生变化?若变化,请找出规律;若不变化,请求出比值.
分析 (1)由∠BPC=∠BPE,∠APD=∠DPE,可得:∠BPD=∠BPE+∠DPE=$\frac{1}{2}$∠APC=40°;
(2)∠ABP:∠AEP的值不发生变化,先由PC∥AB,根据两直线平行内错角相等可得:∠BPC=∠ABP,然后由∠BPC=∠BPE,根据等量代换可得:∠ABP=∠BPE,然后根据三角形外角的性质可得:∠AEP=2∠ABP,进而可得:∠ABP:∠AEP=$\frac{1}{2}$.
解答 解:(1)∵∠BPC=∠BPE,∠APD=∠DPE,且∠BPC+∠BPE+∠APD+∠DPE=∠APC=80°,
∴∠BPD=∠BPE+∠DPE=$\frac{1}{2}$∠APC=40°;
(2)∠ABP:∠AEP的值不发生变化.
理由:∵PC∥AB,
∴∠BPC=∠ABP,
∵∠BPC=∠BPE,
∴∠ABP=∠BPE,
∵∠AEP=∠ABP+∠BPE,
∴∠AEP=2∠ABP,
∴∠ABP:∠AEP=$\frac{1}{2}$.
故将BC平行移动,∠ABP:∠AEP的值不发生变化,其比值为$\frac{1}{2}$.
点评 此题考查了平行线的判定与性质、三角形外角的性质,解题的关键是:熟记同位角相等?两直线平行,内错角相等?两直线平行,同旁内角互补?两直线平行.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.某商品的标价为132元,若以9折出售仍可获利10%,则此商品的进价为( )
| A. | 88元 | B. | 98元 | C. | 108元 | D. | 118元 |
5.在下列四个说法中,正确的有( )个:
①不带根号的数一定是有理数;
②$\root{3}{5}$是一个负数;
③已知a是实数,则$\sqrt{{a}^{2}}$=|a|;
④全体实数和数轴上的点是一一对应.
①不带根号的数一定是有理数;
②$\root{3}{5}$是一个负数;
③已知a是实数,则$\sqrt{{a}^{2}}$=|a|;
④全体实数和数轴上的点是一一对应.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.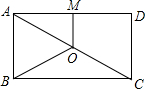 如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )
 如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
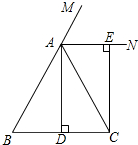 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠ACM的平分线,CE⊥AN,垂足为点E
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠ACM的平分线,CE⊥AN,垂足为点E