题目内容
1.在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,且AD=AB.(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60°,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
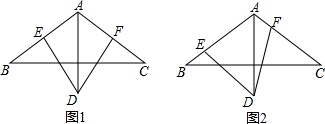
分析 (1)由等腰三角形的性质和已知条件得出∠BAD=∠DAC=$\frac{1}{2}$×120°=60°,再证出∠ADE=∠ADF=90°-60°=30°,由含30角的直角三角形的性质得出AE=$\frac{1}{2}$AD,AF=$\frac{1}{2}$AD,即可得出结论;
(2)连接BD,证明△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠ABD=∠DAC,得出∠EDB=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF,即可得出结论.
解答 (1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC,
∵∠BAC=120°,
∴∠BAD=∠DAC=$\frac{1}{2}$×120°=60°,
∵DE⊥AB,DF⊥AC,
∴∠ADE=∠ADF=90°-60°=30°,
∴AE=$\frac{1}{2}$AD,AF=$\frac{1}{2}$AD,
∴AE+AF=$\frac{1}{2}$AD+$\frac{1}{2}$AD=AD;
(2)解:线段AE,AF,AD之间的数量关系为:AE+AF=AD,理由如下:
连接BD,如图所示:
∵∠BAD=60°,AB=AD,
∴△ABD是等边三角形,
∴BD=AD,∠ABD=∠ADB=60°,
∵∠DAC=60°,
∴∠ABD=∠DAC,
∵∠EDB+∠EDA=∠EDA+∠ADF=60°,
∴∠EDB=∠ADF,
在△BDE与△ADF中,$\left\{\begin{array}{l}{∠ABD=∠DAC}\\{AD=BD}\\{∠EDB=∠ADF}\end{array}\right.$,
∴△BDE≌△ADF(ASA),
∴BE=AF,
∵AE+BE=AD,
∴AE+AF=AD.
点评 本题考查了等腰三角形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30角的直角三角形的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案解:设S=1+51+52+53+54+55+56+57+58+59+510…①
在①式的两边同时都乘以5得:
5S=51+52+53+54+55+56+57+58+59+510+511…②
②-①得:5S-S=511-1,即4S=511-1,∴S=$\frac{{5}^{11}-1}{4}$,得出答案后,爱动脑筋的小明想:如果把“5”换成字母“a”(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2014的值?则求出的答案是( )
| A. | $\frac{{a}^{2014}-1}{a-1}$ | B. | $\frac{{a}^{2014}-1}{a}$ | C. | $\frac{{a}^{2015}-1}{a-1}$ | D. | $\frac{{a}^{2015}-1}{a}$ |
| A. | $\left\{\begin{array}{l}{60x+y=1000}\\{40x-y=1000}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60x-y=1000}\\{40x+y=1000}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y=1000}\\{\frac{40}{60}x+y=1000}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=1000}\\{\frac{40}{60}x-y=1000}\end{array}\right.$ |
| A. | 两直线平行,同旁内角相等 | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 三角形三条边的垂直平分线相交于一点,且这一点到三边的距离相等 | |
| D. | 两角分别相等且其中一组等角的对边相等的两个三角形全等 |
| A. | (-3,-1) | B. | (3,1) | C. | (-3,1) | D. | (-1,3) |