题目内容
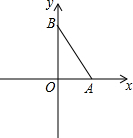 如图,在平面直角坐标系中,点A,B分别在x轴,y轴上,且∠ABO=30°,点P在坐标轴上且使△ABP为等腰三角形,则满足条件的点P共有
如图,在平面直角坐标系中,点A,B分别在x轴,y轴上,且∠ABO=30°,点P在坐标轴上且使△ABP为等腰三角形,则满足条件的点P共有考点:等腰三角形的判定,坐标与图形性质
专题:
分析:分类讨论:P在x轴上,P在y轴上,根据两边相等的三角形是等腰三角形,可得答案.
解答:解:当P在x轴上时,AB=AP时,P点有两个,BP=AP时,P点有一个,AB=BP时,P点有一个
当P在y轴上时,AB=BP时,P点有两个,BP=AP时,P点有一个,AB=AP时,P点有一个,
综上所述:符合条件的P点有8个,
故答案为:8.
当P在y轴上时,AB=BP时,P点有两个,BP=AP时,P点有一个,AB=AP时,P点有一个,
综上所述:符合条件的P点有8个,
故答案为:8.
点评:本题考查了等腰三角形,利用了等腰三角形的判定,分类讨论是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
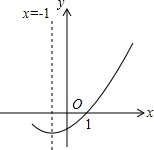 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0②b=2a;③当-3<x<1时,ax2+bx+c<0;④a-b<m(am+b)(m≠-1).其中正确的命题有( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0②b=2a;③当-3<x<1时,ax2+bx+c<0;④a-b<m(am+b)(m≠-1).其中正确的命题有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是( )| A、ac>0 |
| B、b<0 |
| C、2a+b=0 |
| D、b2-4ac<0 |
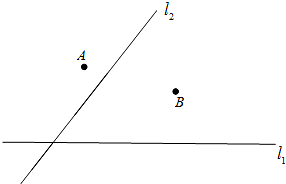 在公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.
在公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.