题目内容
10.解下列方程:(1)-3x2+5x+2=0 (公式法)
(2)x2+6x-4=0 (配方法)
(3)现定义运算“★”,对于任意实数a、b,都有a★b=a2-3a+b,如:3★5=32-3×3+5,若x★2=6,求实数x的值.
分析 (1)找出方程的二次项系数a,一次项系数b及常数项c,计算出根的判别式的值大于0,将a,b,c的值代入求根公式,即可求出方程的解;
(2)根据配方法的步骤先把常数项移到等号的右边,再在等式的两边同时加上一次项系数的一半,配成平方的形式,即可得出答案;
(3)根据新运算的定义得出x2-3x+2=6,再解方程即可.
解答 解:(1)-3x2+5x+2=0,
∵a=-3,b=5,c=2,b2-4ac=25+24=49>0,
∴x=$\frac{-5±\sqrt{49}}{-6}$=$\frac{-5±7}{-6}$,
∴x1=-$\frac{1}{3}$,x2=2;
(2)x2+6x-4=0,
x2+6x=4,
x2+6x+9=4+9,
(x+3)2=13,
x+3=±$\sqrt{13}$,
x1=-3+$\sqrt{13}$,
x2=-3-$\sqrt{13}$;
(3)根据题意得:
若x★2=6,
则x2-3x+2=6,
x2-3x-4=0,
(x+1)(x-4)=0,
x1=-1,x2=4.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
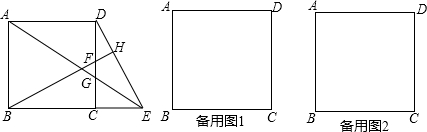
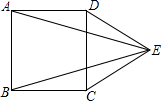 如图,以正方形ABCD的DC边为一边向外作一个等边三角形CDE.
如图,以正方形ABCD的DC边为一边向外作一个等边三角形CDE.