题目内容
小芳想在边长为16cm的等边三角形中剪下一个最大的矩形,她是这样想的,将等边△ABC沿高作AD对折,使AB与AC边重合,在AC上找一个点E作EF⊥DC、EG⊥AD,交DC、AD于F、G,设AE=x,截下GE、EF两边得到的矩形面积最大值为y,请问x为多少时,y取最大值?最大值为多少?
考点:相似三角形的应用,二次函数的最值
专题:
分析:作出图形,根据等边三角形的性质求出AD,EG=
x,再根据相似三角形对应高的比等于相似比求出GD,然后根据矩形的面积公式列式整理,再根据二次函数的最值问题解答.
| 1 |
| 2 |
解答: 解:∵等边△ABC的边长为16cm,
解:∵等边△ABC的边长为16cm,
∴AD=
×16=8
cm,EG=
x,
∵EG⊥AD,
∴△AEG∽△ADC,
∴
=
,
即
=
,
解得GD=8
-
x,
所以,y=(8
-
x)•(2•
x),
=-
(x-8)2+32
,
所以,x=8时,y最大=32
.
 解:∵等边△ABC的边长为16cm,
解:∵等边△ABC的边长为16cm,∴AD=
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∵EG⊥AD,
∴△AEG∽△ADC,
∴
| AG |
| AD |
| EG |
| CD |
即
8
| ||
8
|
| ||
| 8 |
解得GD=8
| 3 |
| ||
| 2 |
所以,y=(8
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=-
| ||
| 2 |
| 3 |
所以,x=8时,y最大=32
| 3 |
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应高的比等于相似比,翻折的性质,二次函数的最值问题,熟记性质是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,它们是一个物体的三视图,该物体的形状是( )
如图,它们是一个物体的三视图,该物体的形状是( )A、 |
B、 |
C、 |
D、 |
 如图,圆锥的侧面积为8πcm2,母线与底面夹角为60°,则此圆锥的高为( )
如图,圆锥的侧面积为8πcm2,母线与底面夹角为60°,则此圆锥的高为( )| A、4cm | ||
| B、8cm | ||
C、2
| ||
| D、6cm |
 如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP.
如图,在△ABC中,∠ABC=90°,点D是AB上一点,且DB=BC,DE平行BC,点P为AC边上的点,DB=DP. 画出如图立体图形的三视图.
画出如图立体图形的三视图.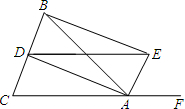 如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE.
如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE.