题目内容
1.当k取何值时,关于x的方程x2-(2k+1)x+k2=2没有实数根?当k取何值时,这个方程有实数根?分析 先把方程化为一般式得到x2-(2k+1)x+k2-2=0,再根据判别式的意义,如果这个方程没有实数根,得到△=[-(2k+1)]2-4(k2-2)<0,然后解不等式;如果这个方程有实数根,得到△=[-(2k+1)]2-4(k2-2)≥0,然后解不等式.
解答 解:方程变形为x2-(2k+1)x+k2-2=0,
如果这个方程没有实数根,得到△=[-(2k+1)]2-4(k2-2)=4k+9<0,
解得k<-$\frac{9}{4}$;
如果这个方程有实数根,得到△=[-(2k+1)]2-4(k2-2)=4k+9≥0,
解得k≥-$\frac{9}{4}$.
故当k<-$\frac{9}{4}$时,关于x的方程x2-(2k+1)x+k2=2没有实数根;当k≥-$\frac{9}{4}$时,这个方程有实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
16.若x、y互为倒数,则用x表示y的正确结果是( )
| A. | x=-y | B. | y=x | C. | y=$\frac{1}{x}$ | D. | y=$±\frac{1}{x}$ |
10.若|a-2|+|b+3|=0,则a-b-1的值为( )
| A. | 4 | B. | -6 | C. | 5 | D. | -7 |
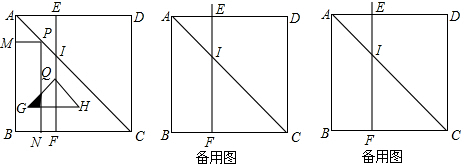
 已知矩形ABCD的面积为10$\sqrt{6}$,求图中阴影部分的面积.
已知矩形ABCD的面积为10$\sqrt{6}$,求图中阴影部分的面积.