题目内容
如图，在5×5的正方形网格中（每个小正方形的边长为1），规定三角形的顶点是网格的交点的三角形叫格点三角形．若格点三角形△DEF和△ABC相似（这里全等除外），△DEF与△ABC的相似比为k，则满足条件的k的值为考点：相似三角形的性质
专题：网格型
分析：作出图形，利用网格计算得出符合题意的k的值．
解答：
解：如图所示：在网格中若格点三角形△DEF和△ABC相似，
设△DEF与△ABC的相似比为k，
当△ABC∽△CBM时，k=
=
；
当△ABC∽△MBN时，k=
=2；
当△ABC∽△DBE时，k=
=
；
当△ABC∽△EBF时，k=
=
；
则满足条件的k的值为：
，2，
，
．
故答案为：
，2，
，
．
解：如图所示：在网格中若格点三角形△DEF和△ABC相似，设△DEF与△ABC的相似比为k，
当△ABC∽△CBM时，k=
| BC |
| AB |
| 2 |
当△ABC∽△MBN时，k=
| MB |
| AB |
当△ABC∽△DBE时，k=
| BD |
| AB |
| 5 |
当△ABC∽△EBF时，k=
| BE |
| AB |
| 10 |
则满足条件的k的值为：
| 2 |
| 5 |
| 10 |
故答案为：
| 2 |
| 5 |
| 10 |
点评：此题主要考查了相似图形的画法，确定三角形的边长后再画图形是解题关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
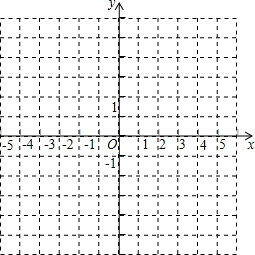如图，在平面直角坐标系xOy中，A（-1.5），B（-1，0），C（-4，3），
如图，一个油桶靠立在直立的墙边，量得WY=0.65cm，并且XY⊥WY．这个油桶的底面半径是多少？为什么？