题目内容
7.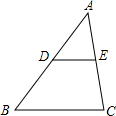 如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,S△ADE=4,则△ABC的面积是多少?
如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,S△ADE=4,则△ABC的面积是多少?
分析 由$\frac{AD}{DB}=\frac{1}{2}$可知$\frac{AD}{AB}=\frac{1}{3}$,由DE∥BC可知△ADE∽△ABC,然后根据相似三角形的面积比等于相似比的平方求解即可.
解答 解:∵$\frac{AD}{DB}=\frac{1}{2}$,
∴$\frac{AD}{AB}=\frac{1}{3}$.
∵DE∥BC,
∴△ADE∽△ABC.
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{AD}{AB})^{2}$,即$\frac{4}{{S}_{△ABC}}=\frac{1}{9}$.
∴S△ABC=36.
点评 根据主要考查的是相似三角形的性质,根据相似三角形的面积比等于相似比的平方求解是解题的关键.

练习册系列答案
相关题目
17.下列方程中,一定是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | 3(x+1)2=2(x+1) | C. | x2-x(x+7)=0 | D. | x+$\frac{1}{x}$=2 |
15.下列各组图形中,一定相似的是( )
| A. | 任意两个矩形 | B. | 任意两个菱形 | ||
| C. | 任意两个直角三角形 | D. | 任意两个等边三角形 |
12.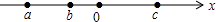 有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
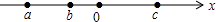 有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b<c | D. | -a-c>-b-c |