题目内容
10.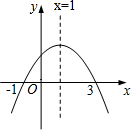 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③④ |
分析 根据二次函数图象与x轴有两个交点得到根的判别式的值大于0,选项①正确;
由对称轴在y轴右侧,得到-$\frac{b}{2a}$=1,变形得到结果,即可对于选项②作出判断;
由对称性得到抛物线与x轴的另一个交点为(3,0),即可得到9a+3b+c=0,即可对于选项③作出判断;
由对称轴为直线x=1,得到a与b的关系,将(-1,0)代入抛物线找出c与b的关系,求出a,b及c的比值,即可对于选项④作出判断.
解答 解:①由抛物线与x轴有两个交点,得到b2-4ac>0,本选项正确;
②由-$\frac{b}{2a}$=1,得到b=-2a,本选项错误;
③由对称性得到x=3时y=0,即9a+3b+c=0,本选项正确;
④由选项②得到b=-2a,再将(-1,0)代入抛物线解析式得:a-b+c=0,即c=b-a=-3a,
∴a:b:c=-1:2:3,本选项正确;
则正确的选项有①③④.
故选:D.
点评 此题考查了二次函数图象与系数的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
1.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a0=1 | C. | (a2)3=a6 | D. | (-3)-2=-$\frac{1}{9}$ |
5. 已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
 已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
已知实数a,b在数轴上的位置如图,则下列等式成立的是( )| A. | b-a>0 | B. | a+b>0 | C. | a-1>0 | D. | 1-b>0 |
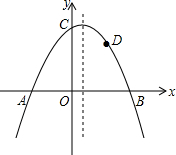 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.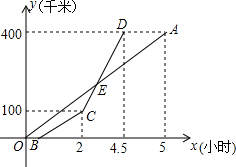 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题: