题目内容
2．
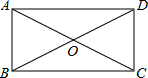如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB=60°，BD=8，则AB的长为（ ）| A． | 4 | B． | $4\sqrt{3}$ | C． | 3 | D． | 5 |
分析 先由矩形的性质得出OA=OB，再证明△AOB是等边三角形，得出AB=OB=4即可．
解答 解：∵四边形ABCD是矩形，
∴OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD=4，AC=BD，
∴OA=OB，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OB=4；
故选：A．
点评 本题考查了矩形的性质、等边三角形的判定与性质；熟练掌握矩形的性质，证明三角形是等边三角形是解决问题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
13．为丰富学生课外活动，某校积极开展社团活动，学生科根据自己的爱好选择一项，已知该校开设的体育社团有：A：篮球，B：排球，C：足球，D：羽毛球，E：乒乓球，李老师对某年级同学选择体育社团的情况进行调查统计，制成了两幅不完整的统计图（如图）．则以下结论正确的是（ ）
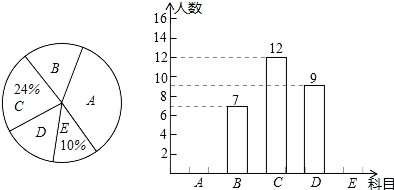
| A． | 选科目E的有10人 | |
| B． | 选科目B的扇形圆心角比选科目D的扇形圆心角的度数多14.4° | |
| C． | 选科目A、B的人数占选体育社团人数的一半 | |
| D． | 选科目A的占34% |
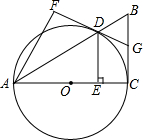如图，已知Rt△ABC中，∠ACB=90°，以AC为直径的圆O交斜边AB于D．过D作DE⊥AC于E，将△ADE沿直线AB翻折得到△ADF．
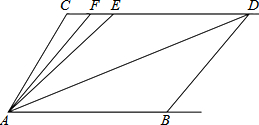如图，已知射线CD∥AB，∠C=∠ABD=110°，E，F在CD上，且满足∠EAD=∠EDA，AF平分∠CAE．