题目内容
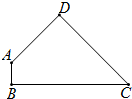 如图,在四边形ABCD中,AB⊥BC,且AD⊥DC,∠A=135°,BC=6,AD=2
如图,在四边形ABCD中,AB⊥BC,且AD⊥DC,∠A=135°,BC=6,AD=2| 3 |
考点:矩形的判定与性质,等腰直角三角形
专题:
分析:根据题意推知△BCE和△AED是等腰直角三角形,则S四边形ABCD=S△BCE-S△AED.
解答: 解:如图,延长BA、CD交于点E.
解:如图,延长BA、CD交于点E.
∵∠DAB=135°,
∴∠EAD=45°.
∵AD⊥DC,
∴∠E=∠EAD=45°.
∴AD=ED=2
,
又∵AB⊥BC,
∴∠C=∠E=45°,
∴BC=BE=6,
∴S四边形ABCD=S△BCE-S△AED=
BC•BE-
AD•ED=
×6×6-
×2
×2
=12.
故答案是:12.
 解:如图,延长BA、CD交于点E.
解:如图,延长BA、CD交于点E.∵∠DAB=135°,
∴∠EAD=45°.
∵AD⊥DC,
∴∠E=∠EAD=45°.
∴AD=ED=2
| 3 |
又∵AB⊥BC,
∴∠C=∠E=45°,
∴BC=BE=6,
∴S四边形ABCD=S△BCE-S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案是:12.
点评:本题考查了等腰直角三角形的判定与性质.此题利用“分割法”求得四边形ABCD的面积.

练习册系列答案
相关题目
如果一个不为零的数的绝对值等于它的相反数,那么这个数是( )
| A、正数 | B、不是负数 |
| C、负数 | D、不是正数 |
 如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,则∠CAE=
如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,则∠CAE= 实数a,b在数轴上的位置如图所示,则a+b
实数a,b在数轴上的位置如图所示,则a+b 如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.若AE=2,则FC=
如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.若AE=2,则FC=