题目内容
如图所示，△ABE≌△ACD，∠B=70°，∠AEB=75°，则∠CAE=考点：全等三角形的性质
专题：
分析：首先计算出∠BAE的度数，再根据全等三角形的性质可得∠BAE=∠CAD=35°，AD=AE，根据等边对等角可得∠ADE=∠AED=75°，进而得到∠CAE的度数．
解答：解：∵∠B=70°，∠AEB=75°，
∴∠BAE=180°-70°-75°=35°，
∵△ABE≌△ACD，
∴∠BAE=∠CAD=35°，AD=AE，
∴∠ADE=75°，
∴∠DAE=30°，
∴∠CAE=35°-30°=5°，
故答案为：5．
∴∠BAE=180°-70°-75°=35°，
∵△ABE≌△ACD，
∴∠BAE=∠CAD=35°，AD=AE，
∴∠ADE=75°，
∴∠DAE=30°，
∴∠CAE=35°-30°=5°，
故答案为：5．
点评：此题主要考查了全等三角形的性质，关键是掌握全等三角形对应边相等，对应角相等．
练习册系列答案
小学课时特训系列答案
相关题目
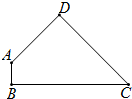如图，在四边形ABCD中，AB⊥BC，且AD⊥DC，∠A=135°，BC=6，AD=