题目内容
在平面直角坐标系中,直线m与两坐标轴围成的三角形的面积为6,与x轴交点的坐标为(-6,0),则直线m的解析式为 .
考点:待定系数法求一次函数解析式
专题:
分析:先画出图形,求出和y轴的交点坐标,设直线m的解析式,把点的坐标代入得出方程组,求出方程组的解即可.
解答:
解:分为两种情况:①设直线m和y轴交于B,与x轴交于A,如图,
∵直线m与两坐标轴围成的三角形的面积为6,与x轴交点的坐标为(-6,0),
∴OA=6,
∴
×6×OB=6,
∴OB=2,
即B的坐标是(0,2),
设直线m的解析式是y=kx+b,
把A、B的坐标代入得:
,
解得:k=
,b=2,
即直线m的解析式为:y=
x+2;
②当直线m和y轴交于C,与x轴交于A时,如图,
同法可求此时直线m的解析式是:y=-
x-2;
故答案为:y=
x+2或y=-
x-2.

解:分为两种情况:①设直线m和y轴交于B,与x轴交于A,如图,
∵直线m与两坐标轴围成的三角形的面积为6,与x轴交点的坐标为(-6,0),
∴OA=6,
∴
| 1 |
| 2 |
∴OB=2,
即B的坐标是(0,2),
设直线m的解析式是y=kx+b,
把A、B的坐标代入得:
|
解得:k=
| 1 |
| 3 |
即直线m的解析式为:y=
| 1 |
| 3 |
②当直线m和y轴交于C,与x轴交于A时,如图,
同法可求此时直线m的解析式是:y=-
| 1 |
| 3 |
故答案为:y=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了三角形的面积,用待定系数法求一次函数的解析式的应用,用了分类讨论思想,题目比较典型,难度适中.

练习册系列答案
相关题目
一个有理数与它的倒数相等,这样的有理数是( )
| A、1,0 | B、-1,0 |
| C、1,-1 | D、-1,0,1 |
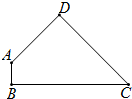 如图,在四边形ABCD中,AB⊥BC,且AD⊥DC,∠A=135°,BC=6,AD=
如图,在四边形ABCD中,AB⊥BC,且AD⊥DC,∠A=135°,BC=6,AD=