题目内容
7.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示有理数的点之间的距离.试探索:(1)求|5-(-2)|=7.
(2)若|x-3|=|x+1|,则x=1.
(3)同样道理|x+5|+|x-2|表示数轴上有理数x所对点到-5和2所对的两点距离之和,请你找出所有符合条件的整数x,使得|x+5|+|x-2|=7,这样的整数是-5,-4,-3,-2,-1,0,1,2.
分析 (1)根据5与-2两数在数轴上所对的两点之间的距离为7得到答案;
(2)根据题意可得方程x-3+x+1=0,再解即可;
(3)由于|x+5|表示x与-5两数在数轴上所对的两点之间的距离,|x-2|表示x与2两数在数轴上所对的两点之间的距离,而|x+5|+|x-2|=7,则x表示的点在-5与2表示的点之间.
解答 解:(1)|5-(-2)|=|5+2|=7,
故答案为:7;
(2)由题意得:x-3+x+1=0,
解得:x=1,
故答案为:1;
(3)∵|x+5|表示x与-5两数在数轴上所对的两点之间的距离,|x-2|表示x与2两数在数轴上所对的两点之间的距离,而-5与2两数在数轴上所对的两点之间的距离为2-(-5)=7,|x+5|+|x-2|=7,
∴-5≤x≤2.
∴x=-5,-4,-3,-2,-1,0,1,2,
故答案为:-5,-4,-3,-2,-1,0,1,2.
点评 本题考查了绝对值和数轴,关键是掌握绝对值的性质:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=-a.

练习册系列答案
相关题目
18. 下面的四幅图案可以通过平移图示得到的是( )
下面的四幅图案可以通过平移图示得到的是( )
 下面的四幅图案可以通过平移图示得到的是( )
下面的四幅图案可以通过平移图示得到的是( )| A. |  | B. |  | C. |  | D. |  |
19.已知点P(3,-2)与点Q关于y轴对称,则点Q的坐标为( )
| A. | (-3,2) | B. | (-3,-2) | C. | (3,2) | D. | (3,-2) |
16.冬季某天我国三个城市的最高气温分别是-11℃,3℃,-3℃,它们任意两城市中最大的温差是( )
| A. | 11℃ | B. | 13℃ | C. | 14℃ | D. | 6℃ |
17.下列说法正确的是( )
| A. | 任何数都有两个平方根 | B. | 若a2=b2,则a=b | ||
| C. | $\sqrt{4}$=±2 | D. | -8的立方根是-2 |
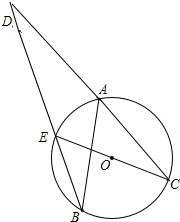 如图,AB、AC是⊙O相等的两弦,延长CA至点D,使AD=AC,连接DB交⊙O于点E,连接CE.证明:CE是⊙O的直径.
如图,AB、AC是⊙O相等的两弦,延长CA至点D,使AD=AC,连接DB交⊙O于点E,连接CE.证明:CE是⊙O的直径.