题目内容
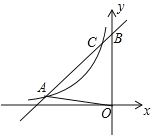
【题目】 如图,在平面直角坐标系中,直线y1=kx+b与x轴交于点A(4,0),与y轴交于点B(0,3),点C是直线y2=![]() x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.
x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.
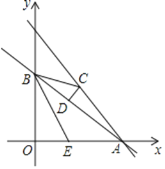
(1)求直线y1=kx+b的函数表达式;
(2)当BC∥x轴时,求BD的长;
(3)点E在线段OA上,OE=![]() OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.
OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)把A、B两点坐标代入y1=kx+b,求出a,b的值即可解决问题;
(2)求出点C的坐标,求出直线CD的解析式,构建方程组确定交点坐标即可.
(3)分两种情形:当∠BCD=∠BEO时,过点A作AM⊥BC交BC的延长线于M,点M作MN⊥x轴于N.当∠CBD=∠BEO时,同法可得点C的横坐标.
(1)把A(4,0),B(0,3)代入y1=kx+b,
得到![]() ,
,
解得: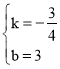 ,
,
∴y1=﹣![]() x+3.
x+3.
(2)∵BC∥x轴,
∴点C的纵坐标为3,
当y=3时,3=﹣![]() x+5,
x+5,
解得x=![]() ,
,
∴C(![]() ,3),
,3),
∵CD⊥AB,
∴直线CD的解析式为y=![]() x+
x+![]() ,
,
由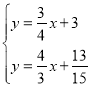 ,解得
,解得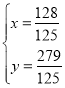 ,
,
∴D(![]() ,
,![]() ),
),
∴BD=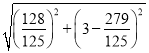 =
=![]() .
.
(3)如图,当∠BCD=∠BEO时,过点A作AM⊥BA交BC的延长线于M,过点M作MN⊥x轴于N.
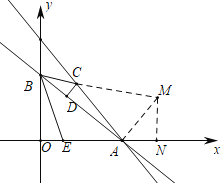
∵OB=3,OE=![]() OA=
OA=![]() ,
,
∴tan∠BEO=![]() =2,
=2,
∵CD⊥AB,AM⊥AB,
∴CD∥AM,
∴∠AMB=∠BCD=∠BEO,
∴tan∠AMB=![]() =2,
=2,
∵AB=![]() =
=![]() =5,
=5,
∴AM=![]() AB=
AB=![]() ,
,
∵∠AOB=∠ANM=∠BAM=90°,
∴∠BAO+∠ABO=90°,∠BAO+∠MAN=90°,
∴∠MAN=∠ABO,
∴△ABO∽△MAN,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AN=![]() ,MN=2,
,MN=2,
∴M(![]() ,2),
,2),
∴直线BM的解析式为y=﹣![]() x+3,
x+3,
由 ,解得x=
,解得x=![]() ,
,
∴点C的横坐标为![]()
如图,当∠CBD=∠BEO时,过点A作AM⊥BA交BC的延长线于M,过点M作MN⊥x轴于N.
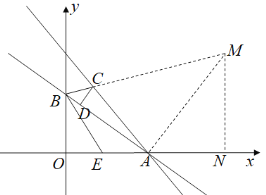
同法可得AM=10,AN=6,MN=8,
∴ON=10,
∴M(10,8),
∴直线BM的解析式为y=![]() x+3,
x+3,
由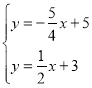 ,解得x=
,解得x=![]() ,
,
∴点C的横坐标为![]()
综上所述,点C的横坐标为![]() 或
或![]() .
.