题目内容
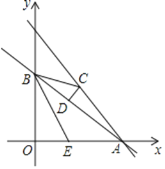
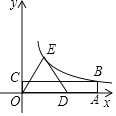
【题目】如图,点![]() 是坐标原点,点
是坐标原点,点![]() 是反比例函数
是反比例函数![]()
![]() 图像上一点,点
图像上一点,点![]() 在
在![]() 轴上,
轴上,![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]() 交反比例函数
交反比例函数![]()
![]() 图像于点
图像于点![]() .
.
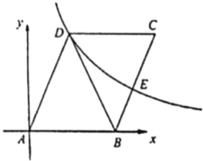
(1)平行四边形![]() 的面积等于______;
的面积等于______;
(2)设![]() 点横坐标为
点横坐标为![]() ,试用
,试用![]() 表示点
表示点![]() 的坐标;(要有推理和计算过程)
的坐标;(要有推理和计算过程)
(3)求![]() 的值;
的值;
(4)求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() ;(4)
;(4)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)如图,作![]() 于
于![]() ,设
,设![]() .先证AB=2m,再根据反比例函数的几何意义求出mn=6,然后根据图形即可确定平行四边形
.先证AB=2m,再根据反比例函数的几何意义求出mn=6,然后根据图形即可确定平行四边形![]() 的面积;
的面积;
(2)由(1)可得CD=AB=2m,再根据四边形![]() 是平行四边形,用m表示出C的坐标,进而得到B的坐标;然后再求出直线BC的解析式,并与
是平行四边形,用m表示出C的坐标,进而得到B的坐标;然后再求出直线BC的解析式,并与![]() 联立,即可确定点E的坐标;
联立,即可确定点E的坐标;
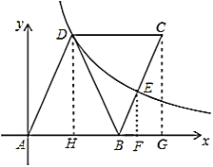
(3)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() .利用平行线分线段成比例定理列方程求解即可;.
.利用平行线分线段成比例定理列方程求解即可;.
(4)由(3)可知![]() ,再求出AD的最小值即可.
,再求出AD的最小值即可.
解:(1)如图,作![]() 于
于![]() ,设
,设![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵点![]() 在
在![]() 上,∴
上,∴![]() ,
,
∴![]() ;
;
(2)由题意![]() ,
,
由(1)可知![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由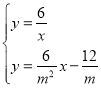 ,解得
,解得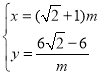 或
或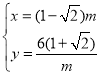 (舍弃),
(舍弃),
∴ ;
;
(3)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() .
.
∵![]() ,
,
∴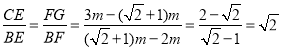 ;
;
(4)∵![]()
∴![]() ,
,
要使得![]() 最小,只要
最小,只要![]() 最小,
最小,
∵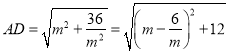 ,
,
∴![]() 的最小值为
的最小值为![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.

【题目】新冠疫情初期,医用口罩是紧缺物资.某市为降低因购买口罩造成人群聚集的感染风险,通过APP实名预约,以摇号抽签的方式,由市民到指定门店购买口罩.规定:已中签者在本轮摇号结束前不再参与摇号;若指定门店当日市民购买口罩的平均等待时间超过8分钟,则次日必须增派工作人员.
(1)据APP数据统计:第一天有386.5万人进行网上预约,此后每天预约新增4万人,且每天有35.5万人中签,若小明第一天没有中签,则他第二天中签的概率是多少?
(2)该市某区指定A,B两门店每天8:00-22:00时段让中签市民排队购买口罩.图1是A门店某日购买口罩的人数与等待时间的统计图,为了算出A门店某日等待9分钟的人数,小红选择14:00~16:00这个时间段到店进行统计,统计结果见表1,且这个时间段的人数占该店当天等待9分钟人数的![]() .表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
.表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
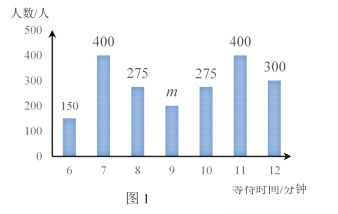
表1
时间段 | 等待9分钟/人 |
14:00~14:30 | 10 |
14:30~15:00 | 20 |
15:00~15:30 | 15 |
15:30~16:00 | 5 |
表2
等待时间 |
|
|
|
|
人数/人 |
|
|
|
|