题目内容
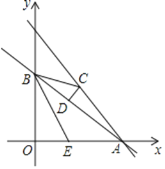
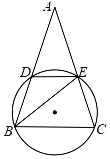
【题目】如图，等腰△ABC两腰AB，AC分别交⊙O于点D，E，点A在⊙O外，点B，C在⊙O上（不与D，E重合），连结BE，DE．已知∠A＝∠EBC，设
＝k（0＜k＜1）．
（1）若∠A＝50°，求
的度数；
（2）若k＝
，求
的值；
（3）设△ABC，△ADE，△BEC的周长分别为c，c1，c2，求证：1＜
≤
．
【答案】（1）30°；（2）
；（3）证明见解析．
【解析】
（1）由等腰三角形的性质可求
，可求
，即可求解；
（2）通过证明
，可求
，设
，则
，
，
，通过证明
，可求
，可求
，即可求解；
（3）由相似三角形的性质可得
，
，可得
，由二次函数的性质可求解．
解：（1）
，
，
，
，
，
的度数
；
（2）
，
，
，
，
，
，
设，则，，
，
四边形
是圆内接四边形，
，
，
，
，
，
，
；
（3）由（2）可得，
，，
，
，
，
由（2）可得，
，
，
，
，
．
练习册系列答案
阅读快车系列答案
相关题目
