题目内容
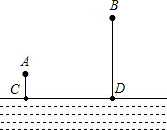 如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.
如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.(1)请你在河CD边上作出水厂位置O,使铺设水管的费用最省;
(2)求出铺设水管的总费用.
考点:轴对称-最短路线问题
专题:
分析:(1)作点A关于河CD的对称点A',连接A'B交河CD于O点,根据轴对称确定最短路线问题,点O就是水厂的位置;
(2)构造出以A′B为斜边的直角三角形,利用勾股定理列式计算即可求出A′B,再乘以单价计算即可得解.
(2)构造出以A′B为斜边的直角三角形,利用勾股定理列式计算即可求出A′B,再乘以单价计算即可得解.
解答: 解:(1)水厂位置O如图所示;
解:(1)水厂位置O如图所示;
(2)如图,作出以A′B为斜边的直角三角形,
∵AC=1km,BD=3km,CD=3km,
∴A′E=CD=3km,BE=3+1=4km,
由勾股定理得,A′B=
=5km,
20 000×5=100 000元.
答:铺设水管的总费用100000元.
 解:(1)水厂位置O如图所示;
解:(1)水厂位置O如图所示;(2)如图,作出以A′B为斜边的直角三角形,
∵AC=1km,BD=3km,CD=3km,
∴A′E=CD=3km,BE=3+1=4km,
由勾股定理得,A′B=
| 32+42 |
20 000×5=100 000元.
答:铺设水管的总费用100000元.
点评:本题考查了轴对称确定最短路线问题,勾股定理,熟练掌握最短路线的确定方法是解题的关键.

练习册系列答案
相关题目
如果单项式
x3ya与xby4是同类项,那么(-a)b的值是( )
| 2 |
| 3 |
| A、64 | B、-64 |
| C、81 | D、-81 |
 如图,点M,N在边长为9的正方形纸片ABCD的边上,将正方形沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,若B′C=3,求AM的长.(提示:连接BM,MB′)
如图,点M,N在边长为9的正方形纸片ABCD的边上,将正方形沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,若B′C=3,求AM的长.(提示:连接BM,MB′) 如图所示:笔直的公路边有甲、乙两栋楼房,高度分别为12m和25m,两楼之间的距离为10m,现有一人沿着公路向这两栋楼房前进,当他走到与甲楼的水平距离为30m且笔直站立时(这种姿势下眼睛到地面的距离为1.6m),他所看到的乙楼上面的部分有多高?
如图所示:笔直的公路边有甲、乙两栋楼房,高度分别为12m和25m,两楼之间的距离为10m,现有一人沿着公路向这两栋楼房前进,当他走到与甲楼的水平距离为30m且笔直站立时(这种姿势下眼睛到地面的距离为1.6m),他所看到的乙楼上面的部分有多高? 如图,直径AB⊥弦CD于E,AE=2cm,CE=4cm.求⊙O半径的长.
如图,直径AB⊥弦CD于E,AE=2cm,CE=4cm.求⊙O半径的长.