题目内容
17．
如图，点D为射线CB上一点，且不与B、C重合，DE∥AB交直线CA延长线于点E（1）作图：过点D作DF∥AC与AB延长线交于点F；
（2）在（1）的条件下，猜想∠EDF与∠BAC的数量关系，并说明理由．
分析 （1）直接利用作一角等于已知角的方法作出∠C=∠CDF，进而得出答案；
（2）利用平行线的性质结合三角形内角和定理进而得出答案．
解答 解：（1）如图所示：
；
（2）∠EDF+∠BAC=180°，
理由：∵DE∥AB，
∴∠E=∠BAC，
∵AC∥DF，
∴∠C=∠FDC，
∵∠C+∠E+∠EDF=180°，
∴∠EDF+∠BAC=180°．
点评 此题主要考查了复杂作图以及平行线的性质和三角形内角和定理，正确作出平行线是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
8．
小红同学将自己5月份的各项消费情况制作成扇形统计图（如图），从图中可看出（ ）
小红同学将自己5月份的各项消费情况制作成扇形统计图（如图），从图中可看出（ ）| A． | 各项消费金额占消费总金额的百分比 | |
| B． | 各项消费的金额 | |
| C． | 各项消费金额的增减变化情况 | |
| D． | 消费的总金额 |
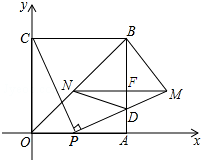如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥AO，交BO于点N，连结ND、BM，设OP=t．
9．下列说法正确的是（ ）
| A． | x2-x=0是二项方程 | B． | $\frac{x-1}{2}-\frac{x}{3}=4$是分式方程 | ||
| C． | $\sqrt{2}{x^2}-2x=\sqrt{3}$是无理方程 | D． | 2x2-y=4是二元二次方程 |