题目内容
9. 如图,在△ABC中,∠B=45°,∠C=30°,AC=6,求AB、BC的长.
如图,在△ABC中,∠B=45°,∠C=30°,AC=6,求AB、BC的长.
分析 过A作AD⊥BC于D,根据直角三角形的性质求出AD,根据勾股定理求出CD、AB,计算即可.
解答 解:过A作AD⊥BC于D,
在Rt△ABC中,∠C=30°,AC=6,
∴AD=$\frac{1}{2}$AC=3,
根据勾股定理得DC=3$\sqrt{3}$,
在Rt△ADB中,∠B=45°,
∴AD=BC=3,
根据勾股定理得AB=3$\sqrt{2}$,
∴BC=BD+DC=3$\sqrt{3}$+3.
点评 本题考查了解直角三角形,解题的关键是作辅助线AD,把原三角形分成两个直角三角形.

练习册系列答案
相关题目
1.下列各数与(-2)3相等的是( )
| A. | 6 | B. | -6 | C. | 8 | D. | -8 |
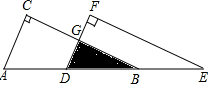 如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.
如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长. 如图,在正方形ABCD中,E、F分别是AD、BC边上的点,且DE=BF,求证:BE=DF.
如图,在正方形ABCD中,E、F分别是AD、BC边上的点,且DE=BF,求证:BE=DF.
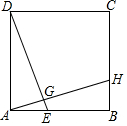 如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.
如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.