题目内容
在平面直角坐标系xOy中,反比例函数y=
的图象与一次函数y=k2x+b的图象交于A(1,5),B(n,-1)两点.
(1)求反比例函数与一次函数的解析式.
(2)当x取何值时,反比例函数的值大于一次函数的值?
(3)求△ABO的面积.
| k1 |
| x |
(1)求反比例函数与一次函数的解析式.
(2)当x取何值时,反比例函数的值大于一次函数的值?
(3)求△ABO的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据待定系数法,可得反比例函数解析式,再根据图象上点的坐标满足函数解析式,可得B点坐标,根据待定系数法,可得一次函数解析式;
(2)根据反比例函数图象在上方的区域,可得答案;
(3)三角形面积的和差,可得答案.
(2)根据反比例函数图象在上方的区域,可得答案;
(3)三角形面积的和差,可得答案.
解答:解:(1)反比例函数y=
的图象过点A(1,5),
∴k1=xy=1×5=5,
∴反比例函数解析式是y=
,
∵B在反比例函数y=
d的图象上,
∴n=
=-5,
∴B点坐标是(-5,-1),
一次函数y=k2x+b的图象过A(1,5),B(-5,-1),
,
解得
,
∴一次函数解析式是y=x+4;
(2)如图:
反比例函数图象在上方的部分:x<-5或0<x<1
(3)S△AOB=S△BOC+S△AOC
=
|-4|×(5+|-1|)
=12.
| k1 |
| x |
∴k1=xy=1×5=5,
∴反比例函数解析式是y=
| 5 |
| x |
∵B在反比例函数y=
| 5 |
| x |
∴n=
| 5 |
| -1 |
∴B点坐标是(-5,-1),
一次函数y=k2x+b的图象过A(1,5),B(-5,-1),
|
解得
|
∴一次函数解析式是y=x+4;
(2)如图:

反比例函数图象在上方的部分:x<-5或0<x<1
(3)S△AOB=S△BOC+S△AOC
=
| 1 |
| 2 |
=12.
点评:本题考查了反比例函数与一次函数交点问题,利用了待定系数法求解析式,利用了图象法解不等式,三角形面积的和差求三角形的面积.

练习册系列答案
相关题目
如图,每个图形都由同样大小的矩形按照一定的规律组成,其中第①个图形的面积为6cm2,第②个图形的面积为18cm2,第③个图形的面积为36cm2,…,那么第⑥个图形的面积为( )
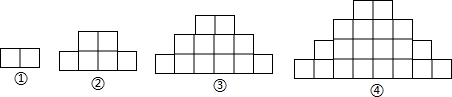

| A、84cm2 |
| B、90cm2 |
| C、126cm2 |
| D、168cm2 |
若a≠0,a,b互为相反数,则不等式ax+b<0的解集为( )
| A、x>1 |
| B、x<1 |
| C、x<1或x>1 |
| D、x<-1或x>-1 |
 解不等式组
解不等式组 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.请在图中方格纸中,按要求完成下列各题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.请在图中方格纸中,按要求完成下列各题: 如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100km..问:A市与C、D两市分别相距多少千米?(结果精确到1km)
如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100km..问:A市与C、D两市分别相距多少千米?(结果精确到1km)