题目内容
6.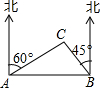 世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.
世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.
分析 作CD⊥AB于D,构造出Rt△ACD与Rt△BCD,求出AB的长度.根据平行线的性质求出三角形各角之间的关系,利用特殊角的三角函数值求解.
解答  解:作CD⊥AB于D.
解:作CD⊥AB于D.
设AD=x,则BD=50×20-x=1000-x.
∵∠EAC=60°,
∴∠CAB=90°-60°=30°.
在Rt△BCD中,
∵∠FBC=45°,
∴∠CBD=∠BCD=45°,
∴CD=DB=1000-x.
在Rt△ACD中,
∵∠CAB=30°,
∴CD=tan30°•AD,
即DB=CD=tan30°•AD=1000-x=$\frac{\sqrt{3}}{3}$x,
解得:x=500(3-$\sqrt{3}$),
故CD=500(3-$\sqrt{3}$)×$\frac{\sqrt{3}}{3}$=500($\sqrt{3}$-1)m.
故答案为:500($\sqrt{3}$-1)m.
点评 此题考查了直角三角形的应用,解答此题的关键是构造出两个特殊角度的直角三角形,再利用特殊角的三角函数值解答.

练习册系列答案
相关题目
17.已知a=2cm,b=10mm,那么$\frac{a}{b}$的值为( )
| A. | $\frac{1}{50}$ | B. | $\frac{1}{5}$ | C. | 2 | D. | $\frac{5}{2}$ |
14.若M是线段AB的黄金分割点(MA>MB),设AB=2cm,则线段MA的长为( )cm.
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | 3-$\sqrt{5}$ | C. | 1 | D. | $\sqrt{5}$-1 |



