题目内容
18. 如图,将1、$\sqrt{2}$、$\sqrt{3}$三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(2014,2014)表示的两个数的积是$\sqrt{3}$.
如图,将1、$\sqrt{2}$、$\sqrt{3}$三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(2014,2014)表示的两个数的积是$\sqrt{3}$.
分析 根据观察数列,可得,每三个数一循环,根据有序数对的表示方法,可得有序数对表示的数,根据是数的运算,可得答案.
解答 解;每三个数一循环,1、$\sqrt{3}$、$\sqrt{2}$,
(8,2)在数列中是第(1+7)×7÷2+2=30个,
30÷3=10,(8,2)表示的数正好是第10轮的最后一个,
即(8,2)表示的数是$\sqrt{3}$,
(2014,2014)在数列中是第(1+2014)×2014÷2=2029105个,
2029105÷3=676368…1,
(2014,2014)表示的数正好是第676369轮的一个数,
即(2014,2014)表示的数是1,
则$\sqrt{3}$×1=$\sqrt{3}$.
故答案为:$\sqrt{3}$
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6.解下列不等式组,结果正确的是( )
| A. | 不等式组$\left\{{\begin{array}{l}{x>7}\\{x>3}\end{array}}\right.$的解集是x>3 | |
| B. | 不等式组$\left\{{\begin{array}{l}{x<-3}\\{x>-2}\end{array}}\right.$的解集是-3<x<-2 | |
| C. | 不等式组$\left\{{\begin{array}{l}{x<-3}\\{x<-1}\end{array}}\right.$的解集是x<-1 | |
| D. | 不等式组$\left\{{\begin{array}{l}{x>-4}\\{x<2}\end{array}}\right.$的解集是-4<x<2 |
3.李老师做了个长方形教具,其中一边长为2a+b,另一边长为a-b,则该长方形的面积为( )
| A. | 6a+b | B. | 2a2-ab-b2 | C. | 3a | D. | 10a-b |
8.解分式方程$\frac{2}{x+1}+\frac{3}{x-1}=\frac{6}{{{x^2}-1}}$,分以下四步,其中,错误的一步是( )
| A. | 方程两边分式的最简公分母是(x-1)(x+1) | |
| B. | 方程两边都乘以(x-1)(x+1),得整式方程2(x-1)+3(x+1)=6 | |
| C. | 解这个整式方程,得x=1 | |
| D. | 原方程的解为x=1 |
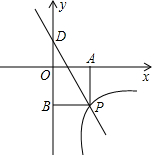 如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数y=$\frac{m}{x}$的图象在第四象限的相交于点P,并且PAx轴于点A,PB⊥y轴于点B,已知B(0,-6),且S△DBP=27
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数y=$\frac{m}{x}$的图象在第四象限的相交于点P,并且PAx轴于点A,PB⊥y轴于点B,已知B(0,-6),且S△DBP=27