Question

18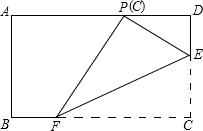．如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC=3DE=3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP=2$\sqrt{3}$a．

Answer 1

分析 作FM⊥AD于M，则MF=DC=3a，由矩形的性质得出∠C=∠D=90°．由折叠的性质得出PE=CE=2a=2DE，∠EPF=∠C=90°，求出∠DPE=30°，得出∠MPF=60°，在Rt△MPF中，由三角函数求出FP即可．

解答 解：作FM⊥AD于M，如图所示：
则MF=DC=3a，
∵四边形ABCD是矩形，
∴∠C=∠D=90°．
∵DC=3DE=3a，
∴CE=2a，
由折叠的性质得：PE=CE=2a=2DE，∠EPF=∠C=90°，
∴∠DPE=30°，
∴∠MPF=180°-90°-30°=60°，
在Rt△MPF中，∵sin∠MPF=$\frac{MF}{FP}$，
∴FP=$\frac{MF}{sin60°}$=$\frac{3a}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$a；
故答案为：2$\sqrt{3}$a．

点评 本题考查了折叠的性质、矩形的性质、三角函数等知识；熟练掌握折叠和矩形的性质，求出∠DPE=30°是解决问题的关键．