题目内容
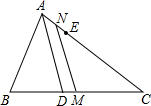 如图,已知AD为△ABC的角平分线,AB<AC,在AC上截取CE=AB,M、N分别为BC、AE的中点.求证:MN∥AD.
如图,已知AD为△ABC的角平分线,AB<AC,在AC上截取CE=AB,M、N分别为BC、AE的中点.求证:MN∥AD.分析:连接BE,记BE中点为F,连接FN、FM,首先根据三角形中位线定理证明FN=FM,再证明∠2=∠5,即可根据同位角相等两直线平行证出结论.
解答: 证明:连接BE,记BE中点为F,连接FN、FM,
证明:连接BE,记BE中点为F,连接FN、FM,
∵FN为△EAB的中位线,
∴FN=
AB,FN∥AB,
∵FM为△BCE的中位线,
∴FM=
CE,FM∥CE,
∵CE=AB,
∴FN=FM,
∴∠3=∠4,
∵∠4=∠5,
∴∠3=∠5,
∵∠1+∠2=∠3+∠5,
∠1=∠2,
∴∠2=∠5,
∴NM∥AD.
 证明:连接BE,记BE中点为F,连接FN、FM,
证明:连接BE,记BE中点为F,连接FN、FM,∵FN为△EAB的中位线,
∴FN=
| 1 |
| 2 |
∵FM为△BCE的中位线,
∴FM=
| 1 |
| 2 |
∵CE=AB,
∴FN=FM,
∴∠3=∠4,
∵∠4=∠5,
∴∠3=∠5,
∵∠1+∠2=∠3+∠5,
∠1=∠2,
∴∠2=∠5,
∴NM∥AD.
点评:此题主要考查了平行线的判定与性质,三角形的中位线定理,解决问题的关键是正确画出辅助线,证明∠2=∠5.

练习册系列答案
相关题目
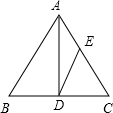 如图,已知AD为等腰三角形ABC底边上的高,且tan∠B=
如图,已知AD为等腰三角形ABC底边上的高,且tan∠B=| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知AD为∠BAC的平分线,且AD=2,AC=
如图,已知AD为∠BAC的平分线,且AD=2,AC= 17、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD=
17、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD=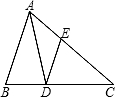 如图,已知AD为△ABC的角平分线,DE∥AB,如果
如图,已知AD为△ABC的角平分线,DE∥AB,如果