题目内容
6.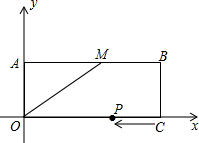 如图,长方形ABCO的顶点A、C、O都在坐标轴上,点B的坐标为(8,3),M为AB的中点.
如图,长方形ABCO的顶点A、C、O都在坐标轴上,点B的坐标为(8,3),M为AB的中点.(1)试求点M的坐标和△AOM的周长;
(2)若P是OC上的一个动点,它以每秒1个单位长度的速度从点C出发沿射线CO方向匀速运动,设运动时间为t秒(t>0).
①若△POM的面积等于△AOM的面积的一半,试求t的值;
②是否存在某一时刻t,使△POM是等腰三角形?若存在,求出此时t的值;若不存在,试说明理由.
分析 (1)根据进行的性质确定点M的坐标,根据勾股定理求出OM的长,求出△AOM的周长;
(2)根据高相等的两个三角形的面积之比等于底的比求出OP的长即可;
(3)分MP=OM、OP=OM和OP=PM三种情况,结合图形、运用相似三角形的判定和性质解答即可.
解答 解:(1)∵四边形ABCO是长方形,点B的坐标为(8,3),M为AB的中点,
∴点M的坐标为(4,3),
由勾股定理求得OM=5,
所以△AOM的周长为3+4+5=12;
(2)∵△POM的面积等于△AOM的面积的一半,
∴OP=$\frac{1}{2}$AM=2,
当点P在原点右侧时,OP=2,则CP=6,
∴t=6,
当点P在原点左侧时,OP=2,则CP=10,
∴t=10,
∴当t=6或t=10时,△POM的面积等于△AOM的面积的一半;
(3)当MP=OM时,点P与点C重合,t=0,
当OP=OM时,OP=5,
当点P在原点右侧时,OP=5,则CP=3,
∴t=3,
当点P在原点左侧时,OP=5,则CP=13,
∴t=13,
当OP=PM时,如图,作PF⊥OM于F,ME⊥OC于E,
∵OP=PM,PF⊥OM,
∴OF=$\frac{1}{2}$OM=$\frac{5}{2}$,
∵PF⊥OM,ME⊥OC,
∴△OFP∽△OEM,
∴$\frac{OP}{OM}$=$\frac{OF}{OE}$,
解得,OP=$\frac{25}{8}$,则CP=$\frac{39}{8}$,
∴t=$\frac{39}{8}$,
∴当t=0、5、13、$\frac{39}{8}$时,△POM是等腰三角形.
点评 本题考查的是矩形的性质、坐标与图形的关系以及等腰三角形的判定定理,灵活运用数形结合思想是解题的关键,注意相似三角形的判定和性质的应用.

练习册系列答案
相关题目
18. 如图,CD是Rt△ABC的中线,∠ACB=90°,AC=8,BC=6,则CD的长是( )
如图,CD是Rt△ABC的中线,∠ACB=90°,AC=8,BC=6,则CD的长是( )
 如图,CD是Rt△ABC的中线,∠ACB=90°,AC=8,BC=6,则CD的长是( )
如图,CD是Rt△ABC的中线,∠ACB=90°,AC=8,BC=6,则CD的长是( )| A. | 2.5 | B. | 3 | C. | 4 | D. | 5 |
16.代数式-3x,0,2x-y,$\frac{2x+y}{4}$,$\frac{3b}{a}$中,单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
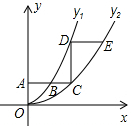 如图,平行于x轴的直线AC分别交函数y1=x2与y2=$\frac{{x}^{2}}{2}$的图象于B,C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则$\frac{DE}{AB}$=2-$\sqrt{2}$.
如图,平行于x轴的直线AC分别交函数y1=x2与y2=$\frac{{x}^{2}}{2}$的图象于B,C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则$\frac{DE}{AB}$=2-$\sqrt{2}$.



 如图,在△ABC中,∠C=28°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A=96°.
如图,在△ABC中,∠C=28°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A=96°.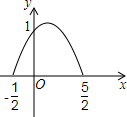 已知一个二次函数y=ax2+bx+c的图象如图所示,请求出这个二次函数的解析式.
已知一个二次函数y=ax2+bx+c的图象如图所示,请求出这个二次函数的解析式.