题目内容
15.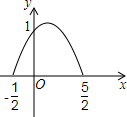 已知一个二次函数y=ax2+bx+c的图象如图所示,请求出这个二次函数的解析式.
已知一个二次函数y=ax2+bx+c的图象如图所示,请求出这个二次函数的解析式.
分析 由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x+$\frac{1}{2}$)(x-$\frac{5}{2}$),然后把(0,1)代入求出a的值即可.
解答 解:设二次函数解析式为y=a(x+$\frac{1}{2}$)(x-$\frac{5}{2}$),
把(0,1)代入得a•$\frac{1}{2}$•(-$\frac{5}{2}$)=1,
解得a=-$\frac{4}{5}$,
所以抛物线解析式为y=-$\frac{4}{5}$(x+$\frac{1}{2}$)(x-$\frac{5}{2}$),即y=-$\frac{4}{5}$x2+$\frac{8}{5}$x+1.
点评 本用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
10. 如图是每个面上都有一个汉字的正方体的表面展开图,在此正方体上与“相”字相对的汉子是( )
如图是每个面上都有一个汉字的正方体的表面展开图,在此正方体上与“相”字相对的汉子是( )
 如图是每个面上都有一个汉字的正方体的表面展开图,在此正方体上与“相”字相对的汉子是( )
如图是每个面上都有一个汉字的正方体的表面展开图,在此正方体上与“相”字相对的汉子是( )| A. | 我 | B. | 能 | C. | 成 | D. | 功 |
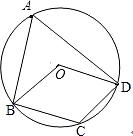 如图,四边形ABCD内接于⊙O,且OB∥DC,OD∥BC,则∠BAD=60°.
如图,四边形ABCD内接于⊙O,且OB∥DC,OD∥BC,则∠BAD=60°.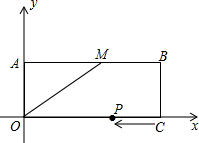 如图,长方形ABCO的顶点A、C、O都在坐标轴上,点B的坐标为(8,3),M为AB的中点.
如图,长方形ABCO的顶点A、C、O都在坐标轴上,点B的坐标为(8,3),M为AB的中点.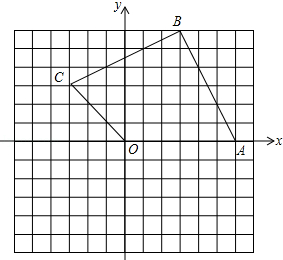 如图在平面直角坐标系中,四边形OABC的顶点分别是O(0,0),A(6,0),B(3,6),C(-3,3).
如图在平面直角坐标系中,四边形OABC的顶点分别是O(0,0),A(6,0),B(3,6),C(-3,3).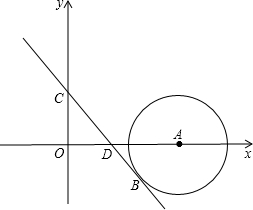 如图.点A在x轴上,且A(4,0),以点A为圆心.2为半径画⊙A,点C坐标为(0,2),CB是⊙A的切线交x轴于点D.
如图.点A在x轴上,且A(4,0),以点A为圆心.2为半径画⊙A,点C坐标为(0,2),CB是⊙A的切线交x轴于点D.