题目内容
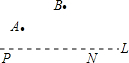某市计划在一条公路L上修建一个火车站P和一个汽车站N，且使两站相距2km，在公路的一侧有景点A，B．如图所示旅客从P站坐车到两处游玩后，直接到N站坐汽车回到P站，则当P站修在公路何处时，能使旅客所走路程最短？考点：轴对称-最短路线问题,作图—应用与设计作图
专题：
分析：求AP+AB+BN+PN的最小值，AB，PN长固定，只要求AP+BN的最小值，利用轴对称和平行四边形的性质即可解答．
解答：
解：过B作BB′∥L，使BB′=2km，作A关于L的对称点A′，连结A′B′交L 于P，P就是所求的点．
∵求AP+AB+BN+PN的最小值，AB，PN长固定，只要求AP+BN的最小值．
∵四边形BB′PN是平等四边形，
∴BN=B′P．
∴P就是所求的点．
解：过B作BB′∥L，使BB′=2km，作A关于L的对称点A′，连结A′B′交L 于P，P就是所求的点．∵求AP+AB+BN+PN的最小值，AB，PN长固定，只要求AP+BN的最小值．
∵四边形BB′PN是平等四边形，
∴BN=B′P．
∴P就是所求的点．
点评：本题考查轴对称及平行四边形的性质等知识的综合应用．综合运用这些知识是解决本题的关键．
练习册系列答案
相关题目
南京市2014年的某10天中，每天的最低气温如图所示（单位：℃），则这10天中南京市最低气温的众数是在“百度”搜索引擎中输入“济水一中”，能搜到与之相关的结果个数约为104000，这个数用科学记数法表示为（ ）
| A、1.04×103 |
| B、104×103 |
| C、1.04×105 |
| D、0.104×106 |
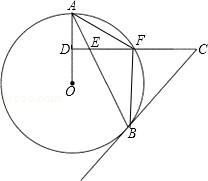如图，AB是⊙O的弦，D为OA半径的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．连结AF、BF．
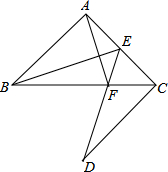如图所示，已知△ABC中，∠BAC=90°，AB=AC，E是AC的中点，CD⊥AC，ED交BC于F．若CD=AB，求证：AF⊥BE．