题目内容
2.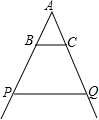 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,BC=20cm,则PQ的长是( )
如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,BC=20cm,则PQ的长是( )| A. | 45cm | B. | 50cm | C. | 60cm | D. | 80cm |
分析 利用相似三角形的判定与性质得出$\frac{AB}{AP}$=$\frac{AC}{AQ}$=$\frac{BC}{PQ}$,进而求出PQ的长.
解答 解:∵BC∥PQ,
∴△ABC∽△APQ,
∴$\frac{AB}{AP}$=$\frac{AC}{AQ}$=$\frac{BC}{PQ}$,
∵AB:AP=2:5,BC=20cm,
∴$\frac{2}{5}$=$\frac{20}{PQ}$,
解得:PQ=50,
故选:B.
点评 此题主要考查了相似三角形的应用,得出△ABC∽△APQ是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
13.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. | 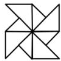 | C. |  | D. |  |
10.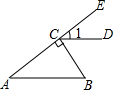 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )| A. | 50° | B. | 40° | C. | 35° | D. | 25° |
14.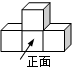 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )
 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
11.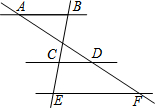 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )| A. | $\frac{36}{5}$ | B. | $\frac{24}{5}$ | C. | $\frac{15}{2}$ | D. | $\frac{9}{2}$ |