题目内容
15.如图a所示,BP平分∠MBN,点D在射线BP上,∠ADC的两边分别交射线BM、BN于A、C两点,且∠ADC+∠MBN=180°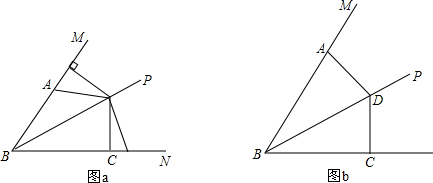
(1)猜想AD与DC之间的数量关系,直接写出你的结论;
(2)如图b是∠ADC绕着点D旋转一定角度得到的,(1)中的结论是否成立?若成立,请证明;若不成立,说明理由.
分析 (1)过D作DP⊥BM于P,DQ⊥BN于N,则∠DOA=∠DQC=90°,于是得到∠PDQ+∠MBN=180°,根据角平分线的性质得到∠ADC+∠MBN=180°,得到∠PDA=∠QDC,证出△ADP≌△CDQ,即可得到结论;
(2)如图2,过D作DP⊥BM于P,DQ⊥BN于N,方法同(1).
解答 解:(1)猜想:AD=DC,
过D作DE⊥BM于P,DQ⊥BN于N,
∴∠DOA=∠DQC=90°,
∴∠PDQ+∠MBN=180°,
∵BP平分∠MBN,
∴DP=DQ,
∵∠ADC+∠MBN=180°,
∴∠ADC=∠PDQ,
∴∠PDA=∠QDC,
在△ADP与△CDQ中,
$\left\{\begin{array}{l}{∠APD=∠DQC}\\{DP=DQ}\\{∠ADP=∠CDQ}\end{array}\right.$,
∴△ADP≌△CDQ,
∴AD=CD;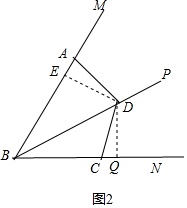
(2)成立,
如图2,过D作DE⊥BM于P,DQ⊥BN于N,
∴∠DOA=∠DQC=90°,
∴∠PDQ+∠MBN=180°,
∵BP平分∠MBN,
∴DP=DQ,
∵∠ADC+∠MBN=180°,
∴∠ADC=∠PDQ,
∴∠PDA=∠QDC,
在△ADP与△CDQ中,
$\left\{\begin{array}{l}{∠APD=∠DQC}\\{DP=DQ}\\{∠ADP=∠CDQ}\end{array}\right.$,
∴△ADP≌△CDQ,
∴AD=CD.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目

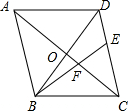 如图,菱形ABCD的周长为20,对角线AC、BD交于点O,BD=6,点E在CD上,DE:EC=2:3,BE交AC于点F,则FC的长为3.
如图,菱形ABCD的周长为20,对角线AC、BD交于点O,BD=6,点E在CD上,DE:EC=2:3,BE交AC于点F,则FC的长为3.