题目内容
某衬衣店将进价为30元的一种衬衣以40元售出,平均每月能售600件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件.
(1)写出月销售利润y(单位:元)与售价x(单位:元/件)之间的函数解析式.
(2)当销售价定为45元时,计算月销售量和销售利润.
(3)衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,销售价应定为多少?
(4)当销售价定为多少元时会获得最大利润?求出最大利润.
(1)y=-10x2+1300x-30000;(2)销售价为45元,月销量550件,销售利润8250元;(3)售价50元;(4)当每件衬衣售价为65元时,月最大利润为12250元. 【解析】试题分析:(1)、根据总利润=单件利润×数量得出函数解析式;(2)、将x=45代入解析式求出答案;(3)、将y=10000代入函数解析式求出x的值;(4)、将二次函数配方成顶点式,从而得出最大值. ...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二次函数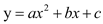 自变量x与函数值y之间满足下列数量关系:
自变量x与函数值y之间满足下列数量关系:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
那么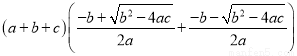 的值为( )
的值为( )
A. -2 B. -1 C. 0 D. 1
A 【解析】根据表中的数据可知,抛物线的对称轴是x=?=1,则?=2.当x=1时,y=a+b+c=?1, 则(a+b+c) =? (a+b+c)=2×(?1)=?2, 故选:A.


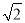 ,x2=﹣
,x2=﹣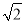
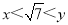 ,则x+y的值是 ________;
,则x+y的值是 ________;
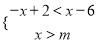 的解集是x>4,那么m的取值范围是 ( ).
的解集是x>4,那么m的取值范围是 ( ).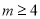 B.
B. 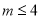 C. m<4 D. m=4
C. m<4 D. m=4