题目内容
4．已知正比例函数的图象A（2，4）、B（a，-2），求该函数表达式及a的值．分析 设正比例函数解析式为y=kx（k≠0），把点A（2，4）代入求出k的值，得出正比例函数的解析式，然后把点B（a，-2）代入正比例函数的解析式，求出a的值即可．
解答 解：设正比例函数解析式为y=kx（k≠0）．
∵正比例函数的图象经过点A（2，4），
∴4=2×k，解得k=2，
∴正比例函数解析式为y=2x；
∵正比例函数的图象经过点B（a，-2），
∴-2=2a，解得a=-1．
点评 本题考查的是用待定系数法求正比例函数的解析式，此类题目需灵活运用待定系数法建立函数解析式，然后将点的坐标代入解析式，利用方程解决问题．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14．若关于x的方程3x+2m=1的解与方程-2x-1=5的解相同，则m的值为（ ）
| A． | 5 | B． | -5 | C． | 4 | D． | -4 |
19．下列方程组中，是三元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{a=1}\\{b=2}\\{b-c=3}\\{\;}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=2}\\{y+z=1}\\{z+c=3}\\{\;}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{4x-3y=7}\\{5x-2y=14}\\{2x-y=4}\\{\;}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{xy+z=3}\\{x+yz=5}\\{xy+y=7}\\{\;}\end{array}\right.$ |
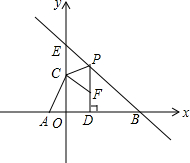如图，B（6，0），E（0，6），直线y=3x+3与x轴、y轴交于A、C两点，∠CPE=∠CAB