题目内容
8．
如图，AB是⊙O的直径，点C在⊙O上（点C不与A、B重合），过点C作⊙O的切线交AB的延长线于点D，连结AC．若∠A=25°，则∠D的度数是40°°．
分析 连接OC．由等腰三角形的性质和三角形的外角的性质可求得∠DOC=50°，接下来，由切线的性质可证明∠OCD=90°，最后在△OCD中依据三角形内角和定理可求得∠D的度数．
解答 解：连接OC．
∵OA=OC，
∴∠A=∠OCA=25°．
∴∠DOC=∠A+∠ACO=50°．
∵CD是⊙的切线，
∴∠OCD=90°．
∴∠D=180°-90°-50°=40°．
故答案为：40．
点评 本题主要考查的是切线的性质、等腰三角形的性质、三角形的外角的性质、三角形的内角和定理，求得∠DOC和∠OCD的度数是解题的关键．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
6．下列调查中，适宜采用普查方式的是（ ）
| A． | 了解一批圆珠笔的寿命 | B． | 了解全国九年级学生身高的现状 | ||
| C． | 检查神舟号载人飞船的各零部件 | D． | 考察人们保护海洋的意识 |
7．小明掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，那么向上一面的点数大于4的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
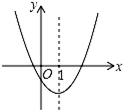如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴是直线x=1，有下列结论：
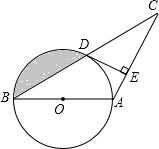已知：如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．
