题目内容
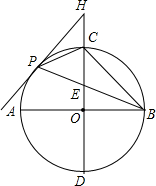 已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是
已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是 |
| AC |
(1)当PH=EH时,求证:直线PH是⊙O的切线;
(2)当E为OC中点时,求PC的长.
考点:切线的判定
专题:证明题
分析:(1)连结OP,如图,由AB⊥CD得到∠1+∠OEB=90°,再证明∠HPE=∠OEB,加上∠1=∠2,得到∠2+∠HPE=90°,然后根据切线的判定定理即可得到直线PH是⊙O的切线;
(2)如图,连结BD,先计算出BD=4
,再由E为OC中点得到OE=CE=2,接着证明△PCE∽△BDE,然后利用相似比可计算出PC的长.
(2)如图,连结BD,先计算出BD=4
| 2 |
解答:(1)证明:连结OP,如图,
∵AB⊥CD,
∴∠1+∠OEB=90°,
∵HP=HE,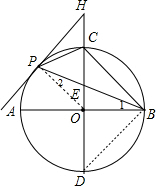
∴∠HPE=∠HEP,
而∠HEP=∠OEB,
∴∠1+∠HPE=90°,
∵OB=OP,
∴∠1=∠2,
∴∠2+∠HPE=90°,即∠OPH=90°,
∴OP⊥PH,
∴直线PH是⊙O的切线;
(2)如图,连结BD,
∵AB⊥CD,OB=OD=4,
∴BD=4
,
∵E为OC中点,
∴OE=CE=2,
∴DE=OE+OD=6,
∵∠CPE=∠D,∠PCE=∠EBD,
∴△PCE∽△BDE,
∴
=
,即
=
,
∴PC=
.
∵AB⊥CD,
∴∠1+∠OEB=90°,
∵HP=HE,

∴∠HPE=∠HEP,
而∠HEP=∠OEB,
∴∠1+∠HPE=90°,
∵OB=OP,
∴∠1=∠2,
∴∠2+∠HPE=90°,即∠OPH=90°,
∴OP⊥PH,
∴直线PH是⊙O的切线;
(2)如图,连结BD,
∵AB⊥CD,OB=OD=4,
∴BD=4
| 2 |
∵E为OC中点,
∴OE=CE=2,
∴DE=OE+OD=6,
∵∠CPE=∠D,∠PCE=∠EBD,
∴△PCE∽△BDE,
∴
| PC |
| BD |
| CE |
| DE |
| PC | ||
4
|
| 2 |
| 6 |
∴PC=
4
| ||
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
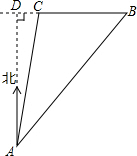 如图,在小岛上有一观测站A,灯塔B在观测站A北偏东45°的方向.灯塔C在灯塔B的正西方向,且相距10海里,灯塔C与观测站A相距10
如图,在小岛上有一观测站A,灯塔B在观测站A北偏东45°的方向.灯塔C在灯塔B的正西方向,且相距10海里,灯塔C与观测站A相距10
 如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等?
如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等? 如图所示,AB=CD,BC=DA,∠1=57°,∠2=43°,则∠B为
如图所示,AB=CD,BC=DA,∠1=57°,∠2=43°,则∠B为 已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC=
已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC= 如图,BD=OD,∠AOC=114°,求∠AOD的度数.
如图,BD=OD,∠AOC=114°,求∠AOD的度数. 如图,已知直线AB,CD相交于点O,EO⊥AB于点O,且∠DOE=8∠COE,求∠BOC和∠BOD的度数.
如图,已知直线AB,CD相交于点O,EO⊥AB于点O,且∠DOE=8∠COE,求∠BOC和∠BOD的度数. 如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是
如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是