题目内容
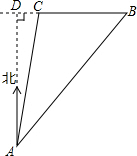 如图,在小岛上有一观测站A,灯塔B在观测站A北偏东45°的方向.灯塔C在灯塔B的正西方向,且相距10海里,灯塔C与观测站A相距10
如图,在小岛上有一观测站A,灯塔B在观测站A北偏东45°的方向.灯塔C在灯塔B的正西方向,且相距10海里,灯塔C与观测站A相距10| 2 |
考点:解直角三角形的应用-方向角问题
专题:
分析:过点C作CE⊥AB,垂足为E,设AE=x,根据锐角三角函数的定义求出CE、AC的长度,再根据∠CAF=∠BAF-∠CAE即可判断出点C的位置.
解答: 解:过点C作CE⊥AB,垂足为E.
解:过点C作CE⊥AB,垂足为E.
∵灯塔B在观察站A北偏东45°的方向,
∴∠B=45°.
又∵BC=10海里
∴在Rt△BCE中,sin∠B=
,
∴sin45°=
,
∴CE=BC•sin45°=10×
=5
(海里).
在Rt△ACE中,
∵AC=10
,
∴sin∠CAE=
=
=
,即sin∠CAE=
,
∴∠CAE=30°
∴∠CAF=∠BAF-∠CAE=45°-30°=15°
答:灯塔C处在观察站A北偏东15°的方向.
 解:过点C作CE⊥AB,垂足为E.
解:过点C作CE⊥AB,垂足为E.∵灯塔B在观察站A北偏东45°的方向,
∴∠B=45°.
又∵BC=10海里
∴在Rt△BCE中,sin∠B=
| CE |
| BC |
∴sin45°=
| CD |
| BC |
∴CE=BC•sin45°=10×
| ||
| 2 |
| 2 |
在Rt△ACE中,
∵AC=10
| 2 |
∴sin∠CAE=
| CE |
| AC |
5
| ||
10
|
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CAE=30°
∴∠CAF=∠BAF-∠CAE=45°-30°=15°
答:灯塔C处在观察站A北偏东15°的方向.
点评:本题考查解直角三角形的应用-方向角问题,解答此题的关键在于根据题意画出示意图,然后根据已知线段利用三角函数的关系进行解答.

练习册系列答案
相关题目
小华掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,则向上的一面的点数小于5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
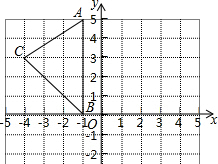 在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).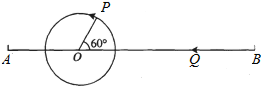 如图,A、B两地相距28个单位长度.AO=8个单位长度,PO=4个单位长度,∠POB=60°,现在点P开始绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q自点B沿BA向点A运动,设点P、Q运动的时间为t(秒).
如图,A、B两地相距28个单位长度.AO=8个单位长度,PO=4个单位长度,∠POB=60°,现在点P开始绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q自点B沿BA向点A运动,设点P、Q运动的时间为t(秒). 如图,∠1与∠2互为补角,∠3=117°.求∠4的度数.
如图,∠1与∠2互为补角,∠3=117°.求∠4的度数.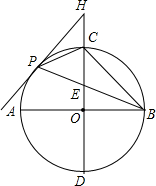 已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是
已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是