题目内容
 如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是
如图,梯形ABCD中,AD∥BC,∠ABC+∠BCD=90°,且BC=3AD,分别以BA、AD、DC为边向梯形外作正方形,其面积分别为S1,S2,S3,则S1,S2,S3之间的关系是考点:勾股定理
专题:
分析:过D点作DE∥AB,那么就可以把这三个正方形的边放在同一个直角三角形里,根据勾股定理即可求出结果.
解答: 解:过D点作DE∥AB,
解:过D点作DE∥AB,
∴四边形ABED是平行四边形,
∴AD=BE,AB=DE,∠B=∠DEC,
∵∠ABC+∠DCB=90°,
∴∠DEC+∠DCE=90°.
∵BC=3AD,
∴2AD=EC,
∵EC2=DE2+DC2,
∴(2AD)2=AB2+DC2,
即4S2=S1+S3.
故答案为:4S2=S1+S3.
 解:过D点作DE∥AB,
解:过D点作DE∥AB,∴四边形ABED是平行四边形,
∴AD=BE,AB=DE,∠B=∠DEC,
∵∠ABC+∠DCB=90°,
∴∠DEC+∠DCE=90°.
∵BC=3AD,
∴2AD=EC,
∵EC2=DE2+DC2,
∴(2AD)2=AB2+DC2,
即4S2=S1+S3.
故答案为:4S2=S1+S3.
点评:本题考查了平行四边形的判定和性质、直角三角形的判定、勾股定理.解题的关键是作辅助线DE,构造平行四边形和直角三角形.

练习册系列答案
相关题目
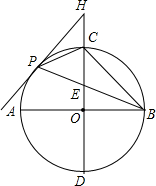 已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是
已知,如图,AB,CD是半径为4的⊙O的两条直径,CD⊥AB,点P是
 如图,四边形ABCD为等腰梯形,双曲线y=
如图,四边形ABCD为等腰梯形,双曲线y=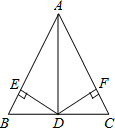 已知:D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别是E、F,DE=DF.
已知:D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别是E、F,DE=DF. 如图,在△ABC中,已知AB=AC,点D在AC上,AD=DB=BC,求∠A的度数.
如图,在△ABC中,已知AB=AC,点D在AC上,AD=DB=BC,求∠A的度数. 已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α
已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α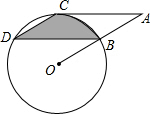 如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB= 如图,点P是等边三角形ABC内一点,PA=1,PB=
如图,点P是等边三角形ABC内一点,PA=1,PB= 如图,⊙O的直径AB和弦CD相交于点E.∠DEB=60°,AE=1,EB=5.试求CD的长.
如图,⊙O的直径AB和弦CD相交于点E.∠DEB=60°,AE=1,EB=5.试求CD的长.