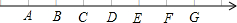题目内容
 如图,在四边形ABCD中,AB=BC,AD=7,∠ADC=∠CBA=90°,tanA=2,求CD的长.
如图,在四边形ABCD中,AB=BC,AD=7,∠ADC=∠CBA=90°,tanA=2,求CD的长.考点:相似三角形的判定与性质,解直角三角形
专题:
分析:如图,作辅助线;证明四边形CDFE为矩形,得到DC=EF(设为2λ),DF=CE;证明AF=λ,BC=2BE(设BE为μ);证明AE=
λ,CE=
μ,运用AB=BC,AD=7,列出关于λ、μ的方程组,即可解决问题.
| 5 |
| 5 |
解答: 解:过点C作CE⊥CD,交AB于点E;
解:过点C作CE⊥CD,交AB于点E;
过点E作EF⊥AD于点F;
则四边形CDFE为矩形,
∴DC=EF(设为2λ),CE∥DF,
DF=CE,∠CEF=90°;
∴∠A=∠CEB;
∵tanA=2,
∴
=
=2,
∴AF=λ,BC=2BE(设BE为μ);
由勾股定理得:AE=
λ,CE=
μ,
∵AB=BC,AD=7,
∴
,
解得:λ=
,
∴CD的长=
.
 解:过点C作CE⊥CD,交AB于点E;
解:过点C作CE⊥CD,交AB于点E;过点E作EF⊥AD于点F;
则四边形CDFE为矩形,
∴DC=EF(设为2λ),CE∥DF,
DF=CE,∠CEF=90°;
∴∠A=∠CEB;
∵tanA=2,
∴
| EF |
| AF |
| BC |
| BE |
∴AF=λ,BC=2BE(设BE为μ);
由勾股定理得:AE=
| 5 |
| 5 |
∵AB=BC,AD=7,
∴
|
解得:λ=
| 7 |
| 6 |
∴CD的长=
| 7 |
| 3 |
点评:该题主要考查了直角三角形的边角关系、勾股定理、矩形的判定及性质等几何知识点的应用问题;解题的关键是作辅助线,构造矩形、直角三角形.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
下列是有理数的是( )
| A、0 | ||
B、
| ||
| C、π | ||
| D、1.010010001…(每两个1之间的0的个数依次多1) |
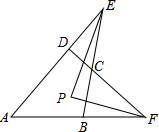 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.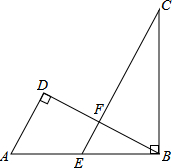 如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2
如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2