题目内容
20.若0°<α<45°,且sinαcosα=$\frac{1}{8}$,求sinα-cosα的值.分析 根据完全平方公式,可得sin2α+cos2α-2sinαcosα,根据sin2α+cos2α=1,根据开方运算,可得答案.
解答 解:0°<α<45°,得sinα<cosα,
sinα-cosα=-$\sqrt{(sinα-cosα)^{2}}$
=-$\sqrt{si{n}^{2}α+co{s}^{2}α-2sinαcosα}$
=-$\sqrt{1-2×\frac{1}{8}}$
=-$\frac{\sqrt{3}}{2}$.
点评 本题考查了同角三角函数关系,利用完全平方公式得出sin2α+cos2α-2sinαcosα是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,在△ABC中,∠C=90°,∠BAC=70°,将△ABC绕点A顺时针旋转70°,B、C旋转后的对应点分别是B′和C′,连接BB′,则∠BB′C′的度数是( )
如图,在△ABC中,∠C=90°,∠BAC=70°,将△ABC绕点A顺时针旋转70°,B、C旋转后的对应点分别是B′和C′,连接BB′,则∠BB′C′的度数是( )
 如图,在△ABC中,∠C=90°,∠BAC=70°,将△ABC绕点A顺时针旋转70°,B、C旋转后的对应点分别是B′和C′,连接BB′,则∠BB′C′的度数是( )
如图,在△ABC中,∠C=90°,∠BAC=70°,将△ABC绕点A顺时针旋转70°,B、C旋转后的对应点分别是B′和C′,连接BB′,则∠BB′C′的度数是( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
5. 如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
 如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
如图可以用来反映这样一个实际情况,一艘船从甲地航行到乙地,达到乙地后即返回,这里横坐标表示航行的时间,纵坐标表示船只与甲地的距离,你认为,船只从甲地到乙地航行的速度与返航的速度是否相同?说说理由.
10.下列各有理数中,最小的数是( )
| A. | -1 | B. | 2 | C. | 0 | D. | -$\frac{1}{2}$ |
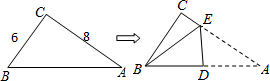 直角三角形纸片的两直角边长分别为6、8 现将△ABC如图那样折叠,使点A与点、B重合,折痕为DE,求cos∠CBE的值.
直角三角形纸片的两直角边长分别为6、8 现将△ABC如图那样折叠,使点A与点、B重合,折痕为DE,求cos∠CBE的值.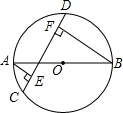 如图,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD于E,BF⊥CD于F
如图,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD于E,BF⊥CD于F 如图,把线段AB平移到线段A′B′,AB与A′B′平行吗?请说明理由.
如图,把线段AB平移到线段A′B′,AB与A′B′平行吗?请说明理由.