题目内容
10．
如图，在△ABC中，∠C=90°，∠BAC=70°，将△ABC绕点A顺时针旋转70°，B、C旋转后的对应点分别是B′和C′，连接BB′，则∠BB′C′的度数是（ ）| A． | 35° | B． | 40° | C． | 45° | D． | 50° |
分析 首先在△ABB'中根据等边对等角，以及三角形内角和定理求得∠ABB'的度数，然后在直角△BB'C中利用三角形内角和定理求解．
解答 解：∵AB=AB'，
∴∠ABB'=∠AB'B=$\frac{180°-∠BAB'}{2}$=$\frac{180°-70°}{2}$=55°，
在直角△BB'C中，∠BB'C=90°-55°=35°．
故选A．
点评 本题考查了旋转的性质，在旋转过程中根据旋转的性质确定相等的角和相等的线段是关键．
练习册系列答案
相关题目
如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE=13，BF=5，则CD的长是（ ）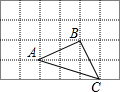
如图是单位长度为1的正方形网格，点A、B、C都在格点上；