ÌâÄ¿ÄÚÈÝ
9£®£¨1£©¼ÆË㣺$\frac{1}{1¡Á2}+\frac{1}{2¡Á3}+$$\frac{1}{3¡Á4}+$¡£®+$\frac{1}{9¡Á10}$£¨2£©¼ÆË㣺$\frac{1}{1¡Á3}+$$\frac{1}{3¡Á5}+\frac{1}{5¡Á7}+$¡£®+$\frac{1}{2015¡Á2017}$
£¨3£©»¯¼ò£º$\frac{1}{m¡Á£¨m+n£©}+\frac{1}{£¨m+n£©£¨m+2n£©}+\frac{1}{£¨m+2n£©£¨m+3n£©}+¡+\frac{1}{£¨m+99n£©£¨m+100n£©}$£®
·ÖÎö £¨1£©ÔʽÀûÓòðÏî·¨±äÐΣ¬µÖÏûºÏ²¢¼´¿ÉµÃµ½½á¹û£»
£¨2£©ÔʽÀûÓòðÏî·¨±äÐΣ¬µÖÏûºÏ²¢¼´¿ÉµÃµ½½á¹û£»
£¨3£©ÔʽÀûÓòðÏî·¨±äÐΣ¬µÖÏûºÏ²¢¼´¿ÉµÃµ½½á¹û£®
½â´ð ½â£º£¨1£©Ôʽ=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+¡+$\frac{1}{9}$-$\frac{1}{10}$=1-$\frac{1}{10}$=$\frac{9}{10}$£»
£¨2£©Ôʽ=$\frac{1}{2}$¡Á£¨1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+¡+$\frac{1}{2015}$-$\frac{1}{2017}$£©=$\frac{1}{2}$¡Á$\frac{2016}{2017}$=$\frac{1008}{2017}$£»
£¨3£©Ôʽ=$\frac{1}{n}$£¨$\frac{1}{m}$-$\frac{1}{m+n}$+$\frac{1}{m+n}$-$\frac{1}{m+2n}$+¡+$\frac{1}{m+99n}$-$\frac{1}{m+100n}$£©=$\frac{1}{n}$£¨$\frac{1}{m}$-$\frac{1}{m+100n}$£©=$\frac{100}{m£¨m+100n£©}$£®
µãÆÀ ´ËÌ⿼²éÁËÓÐÀíÊýµÄ»ìºÏÔËË㣬ÊìÁ·ÕÆÎÕÔËËã·¨ÔòÊǽⱾÌâµÄ¹Ø¼ü£®

 ¾ÙÒ»·´ÈýÆÚÄ©°Ù·Ö³å´Ì¾íϵÁдð°¸
¾ÙÒ»·´ÈýÆÚÄ©°Ù·Ö³å´Ì¾íϵÁдð°¸| A£® | 22014 | B£® | 22015 | C£® | 22016 | D£® | 4032 |
| A£® | ÈýÌõ±ßµÄ´¹Ö±Æ½·ÖÏߵĽ»µã | B£® | ÈýÌõ½Çƽ·ÖÏߵĽ»µã | ||
| C£® | ÈýÌõÖÐÏߵĽ»µã | D£® | ÈýÌõ¸ßµÄ½»µã |
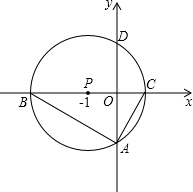 Èçͼ£¬ÒÔµãP£¨-2£¬0£©ÎªÔ²ÐĵÄÔ²£¬½»xÖáÓÚB¡¢CÁ½µã£¨BÔÚCµÄ×ó²à£©£¬½»yÖáÓÚA¡¢DÁ½µã£¨AÔÚDµÄÏ·½£©£¬AD=4$\sqrt{3}$£¬½«¡÷ABCÈƵãPÐýת180¡ã£¬µÃµ½¡÷MCB£®
Èçͼ£¬ÒÔµãP£¨-2£¬0£©ÎªÔ²ÐĵÄÔ²£¬½»xÖáÓÚB¡¢CÁ½µã£¨BÔÚCµÄ×ó²à£©£¬½»yÖáÓÚA¡¢DÁ½µã£¨AÔÚDµÄÏ·½£©£¬AD=4$\sqrt{3}$£¬½«¡÷ABCÈƵãPÐýת180¡ã£¬µÃµ½¡÷MCB£®