题目内容
17．计算：（1）$\sqrt{12}+3\sqrt{48}-24\sqrt{\frac{1}{3}}$；
（2）$\sqrt{42}+\sqrt{7}×\sqrt{\frac{27}{2}}$．
分析 （1）先进行二次根式的化简，然后合并；
（2）先进行二次根式的乘法运算，然后化简合并．
解答 解：（1）原式=2$\sqrt{3}$+12$\sqrt{3}$-8$\sqrt{3}$
=6$\sqrt{3}$；
（2）原式=$\sqrt{42}$+$\frac{3\sqrt{42}}{2}$
=$\frac{5}{2}$$\sqrt{42}$．
点评 本题考查了二次根式的混合运算，解答本题的关键是掌握二次根式的化简和合并．
练习册系列答案
名校课堂系列答案
相关题目
8．
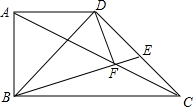如图，直角梯形ABCD中，AD∥BC，AD=AB，AB⊥BC，BC=2AD，E为CD的中点，BE、AC交于点F，连接DF．下列结论：①△BCD为等腰直角三角形；②△ABC∽△EDB；③DF⊥BE；④AF=$\sqrt{2}$CF．其中正确的结论个数是（ ）
如图，直角梯形ABCD中，AD∥BC，AD=AB，AB⊥BC，BC=2AD，E为CD的中点，BE、AC交于点F，连接DF．下列结论：①△BCD为等腰直角三角形；②△ABC∽△EDB；③DF⊥BE；④AF=$\sqrt{2}$CF．其中正确的结论个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
5．下列式子正确的是（ ）
| A． | $\sqrt{3}+\sqrt{4}=\sqrt{7}$ | B． | $\sqrt{2}+\sqrt{5}=\sqrt{10}$ | C． | $\sqrt{48}=4\sqrt{3}$ | D． | 2$\sqrt{6}-\sqrt{6}$=2 |
12．在同一时刻，一幢25米的高楼，影长为20米，那么此时一根高10米的旗杆，影长为（ ）米．
| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
如图是由7个完全相同的小立方块搭成的几何体，已知每个小立方块的棱长为2cm．
如图，已知AB∥CF，E为DF的中点，若AB=7cm，BD=3cm，则CF=4cm．
6．下列条件中，能作出唯一三角形的是（ ）
| A． | 已知两边 | B． | 已知两角 | C． | 已知两边一角 | D． | 已知两角一边 |