题目内容
7．化简：（$\frac{x+1}{x}$-$\frac{x}{x-1}$）÷$\frac{1}{（x-1）^{2}}$．分析 先将括号内两分式通分、将除法转化为乘法，再计算括号内分式的减法，最后约分可得．
解答 解：原式=[$\frac{（x+1）（x-1）}{x（x-1）}$-$\frac{{x}^{2}}{x（x-1）}$]•（x-1）2
=$\frac{-1}{x（x-1）}$•（x-1）2
=$\frac{1-x}{x}$．
点评 本题主要考查分式的混合运算，熟练掌握分式的混合运算顺序及依据分式的基本性质对分式通分、约分是解题的关键．
练习册系列答案
相关题目
20．
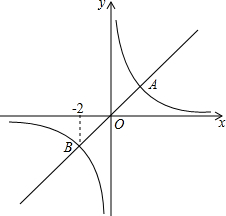正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点B的横坐标为-2，当y1＜y2时，x的取值范围是（ ）
正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点B的横坐标为-2，当y1＜y2时，x的取值范围是（ ）| A． | x＜-2或x＞2 | B． | x＜-2或0＜x＜2 | C． | -2＜x＜0或0＜x＜2 | D． | -2＜x＜0或x＞2 |
如图，已知O是直线MN上的一点，∠AOB=90°，经过点O的直线DC平分∠BON，∠1=38°，求∠3和∠DOA的度数．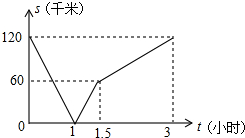
甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：干米），甲行驶的时间为s（单位：小时），s与t之间的函数关系如图所示，有下列结论：（汽车速度大于摩托车速度）．①出发1小时，甲、乙在途中相遇；②出发1.5小时，甲行驶了60千米；③出发2小时，甲、乙相距8O干米；④出发3小时，甲、乙同时到达目的地；其中，正确结论的个数是（ ）
16．用甲、乙两种原料配制成某种饮料，已知这两种原料的维生素C的含量及购买这两种原料的价格如下表所示：
（1）现配制这种饮料10kg，要求至少含有4200单位的维生素C，写出所需甲种原料的质量x（kg）应满足的不等式．
（2）如果仅要求购买甲、乙两种原料的费用不超过72元，求所需甲种原料的质量x（kg）的取值范围．
| 原料 | 甲 | 乙 |
| 维生素C的含量∕（单位∕kg） | 600 | 100 |
| 原料价格∕（元∕kg） | 8 | 4 |
（2）如果仅要求购买甲、乙两种原料的费用不超过72元，求所需甲种原料的质量x（kg）的取值范围．
如图，AB=10cm，点C、D在AB上，且CB=4cm，D是AC的中点．