题目内容
19.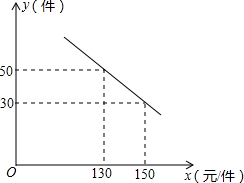 某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:(1)求出y与x之间的函数关系式;
(2)当销售单价定为多少元时,每天可获得700元的利润.
分析 (1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于k、b的关系式,求出k、b的值即可;
(2)根据每天可获得700元的利润列出方程,解方程即可.
解答 解:(1)设y与x之间的函数关系式为y=kx+b(k≠0).
由所给函数图象可知,$\left\{\begin{array}{l}130k+b=50\\ 150k+b=30\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=180\end{array}\right.$,
故y与x的函数关系式为y=-x+180;
(2)∵y=-x+180,依题意得
∴(x-100)(-x+180)=700,
x2-280x+18700=0,
解得x1=110,x2=170.
∵100≤x≤160,
∴取x=110.
答:售价定为110元/件时,每天可获利润700元.
点评 本题考查了一元二次方程的应用、一次函数的应用、待定系数法确定一次函数的解析式;根据题意列出关于k、b的关系式和列出方程是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.如果a>b,那么下列不等式中正确的是( )
| A. | a-b<0 | B. | a+3<b-3 | C. | ac2>bc2 | D. | 3-a<3-b |
4.不等式组$\left\{\begin{array}{l}{x>-1}\\{x>2}\end{array}\right.$的解集是( )
| A. | x>-1 | B. | -1<x<2 | C. | x>2 | D. | x<2 |
9.北京在2015年6月初申办2022冬季奥运会的陈述中表示,若申办成功,这项活动将带动的3.2亿人参与,将3.2亿用科学记数法表示为( )
| A. | 32×107 | B. | 3.2×108 | C. | 3.2×109 | D. | 0.32×1010 |