题目内容
 如图,在7×7网格纸中,每个小正方形的边长都为1.
如图,在7×7网格纸中,每个小正方形的边长都为1.(1)请在网格纸中建立平面直角坐标系,使点A、C的坐标分别为(1,2),(2,0),并写出点B的坐标为
(2)求图中格点△ABC的面积;
(3)判断△ABC的形状,并证明你的结论.
考点:勾股定理,坐标与图形性质,勾股定理的逆定理
专题:
分析:(1)根据题意建立直角坐标系,根据点B在坐标系中的位置写出B点坐标即可;
(2)利用正方形的面积减去三个顶点上三角形的面积即可;
(3)根据勾股定理的逆定理判断出△ABC的形状即可.
(2)利用正方形的面积减去三个顶点上三角形的面积即可;
(3)根据勾股定理的逆定理判断出△ABC的形状即可.
解答: 解:(1)如图所示,
解:(1)如图所示,
由图可知,B(-2,-2).
故答案为(-2,-2);
(2)S△ABC=42-
×4×2-
×1×2-
×4×3=16-4-1-6=5.
(3)结论:△ABC是直角三角形.
证明:∵AB2=32+42=25,BC2=42+22=20,AC2=22+12=5.
∴BC2+AC2=20+5=25=AB2,
∴△ABC是直角三角形.
 解:(1)如图所示,
解:(1)如图所示,由图可知,B(-2,-2).
故答案为(-2,-2);
(2)S△ABC=42-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)结论:△ABC是直角三角形.
证明:∵AB2=32+42=25,BC2=42+22=20,AC2=22+12=5.
∴BC2+AC2=20+5=25=AB2,
∴△ABC是直角三角形.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
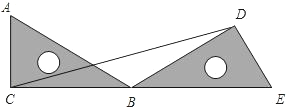 如图,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一个直角三角形ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合. 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,此时AN的长约是(参考:
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气道步行1000米到达点C处,测得M小区位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,此时AN的长约是(参考:
 在等腰直角△ABC中,∠C=90°,AC=6,D为AC上一点,若tan∠DBC=
在等腰直角△ABC中,∠C=90°,AC=6,D为AC上一点,若tan∠DBC=