题目内容
14.如图(1),在矩形ABCD中,AD=6,AB=8,点E是AB边上-动点(点E不与点A、B重合),过点E作EF∥AC交BC于点F,连接ED.(1)设AE=x,则EF=$\frac{5}{4}$(8-x);
(2)若DE⊥EF,求EF的长;
(3)如图(2),过点E作EG⊥EF.交AC于点H,交直线CD于点G,连接AG、FG,随着点E在线段AB上的运动,当AE为何值时,△EFG与△AHE相似?
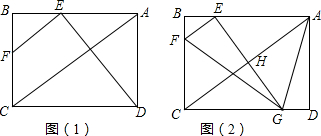
分析 (1)首先由在矩形ABCD中,AD=6,AB=8,可求得AC的长,然后由EF∥AC,证得△BEF∽△BAC,再利用相似三角形的对应边成比例,即可求得答案;
(2)由DE⊥EF,易证得△ADE∽△BAC,再利用相似三角形的对应边成比例,即可求得EF的长;
(3)首先过点G作GH⊥AB于点H,可求得GH的长,由EG⊥EF,易证得△HGE∽△BAC,则可求得EH的长,然后分别从△EFG∽△HAE与△EFG∽△HEA,去分析求解即可求得答案.
解答 解:(1)∵在矩形ABCD中,AD=6,AB=8,
∴BC=AD=6,∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵EF∥AC,
∴△BEF∽△BAC,
∴$\frac{EF}{AC}=\frac{BE}{AB}$,
∵AE=x,
∴BE=AB-AE=8-x,
∴$\frac{EF}{10}=\frac{8-x}{8}$,
解得:EF=$\frac{5}{4}$(8-x);
故答案为:$\frac{5}{4}$(8-x);
(2)∵DE⊥EF,
∴∠BEF+∠AED=90°,
∵∠AED+∠ADE=90°,
∴∠BEF=∠ADE,
∵EF∥AC,
∴∠BEF=∠BAC,
∵∠DAE=∠ABC=90°,
∴△ADE∽△BAC,
∴$\frac{AE}{BC}=\frac{AD}{AB}$,
即$\frac{x}{6}=\frac{6}{8}$,
解得:x=$\frac{9}{2}$,
∴EF=$\frac{5}{4}$(8-x)=$\frac{35}{8}$;
(3)过点G作GM⊥AB于点M,
则四边形ADGM是矩形,
∴GM=AD=6,
∵EF⊥EG,
∴∠GEM+∠BEF=90°,
∵∠GEM+∠EGH=90°,
∴∠EGM=∠BEF,
∵∠EMG=∠B=90°,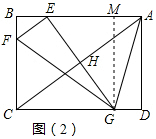
∴△EGM∽△FBE,
∵EF∥AC,
∴△BEF∽△BAC,
∴△MGE∽△BAC,
∴$\frac{EG}{AC}=\frac{GM}{AB}$,
∴$\frac{EG}{10}=\frac{6}{8}$,
解得:EG=$\frac{15}{2}$,
∵EF⊥EG,EF∥AC,
∴EG⊥AC,
∴△AEH∽△ACB,
∴$\frac{AH}{EH}=\frac{AB}{BC}$=$\frac{8}{6}$=$\frac{4}{3}$,
若△EFG∽△HEA,
则$\frac{EF}{EG}=\frac{EH}{AH}$,
∴$\frac{EF}{\frac{15}{2}}=\frac{3}{4}$,
解得:EF=$\frac{45}{8}$;
∴AE=x=$\frac{7}{2}$;
若△EFG∽△HAE,
则$\frac{EF}{EG}=\frac{AH}{EH}$=$\frac{4}{3}$,
解得:EF=10,
此时x=0,不符合题意,舍去.
∴当AE=$\frac{7}{2}$时,△EFG与△AHE相似.
点评 此题考查了相似三角形的判定与性质、矩形的性质以及直角三角形的性质.注意准确作出辅助线、充分利用相似三角形的对应边成比例是解此题的关键.

| A. | 4a2-2a2=2a2 | B. | (a2)3=a5 | C. | a2•a3=a6 | D. | a3+a2=a5 |
| A. |  | B. |  | C. |  | D. |  |
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | -1 | D. | 1 |

