题目内容
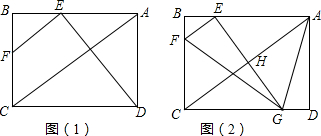
2.如图1是一副三角尺拼成的图案(1)求∠EBC的度数;
(2)将图1中的三角尺ABC绕B旋转20度,∠CBE=130°或170°(图2)
(3)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,求出∠EBC的度数;若不能,说明理由.

分析 (1)∠EBC是由一个直角和一个60°的角组成的;
(2)分不同方向旋转,求解.
(3)根据等量关系∠ABE=2∠DBC,求出α,进而求解.
解答 解:(1)∠EBC=∠ABC+∠EBD=60°+90°=150°,
(2)逆时针旋转时,∠CBE=∠EBA+∠ABD+∠DBC=70°+20°+40°=130°,
顺时针旋转时,∠CBE=∠EBD+∠DBA+∠ABC=90°+20°+60°=170°,
故答案为130°或170°.
(3)第一种情况:
若逆时针旋转α度(0<α<60°),
据题意得90°-α=2(60°-α),
得α=30°,
∴∠EBC=90°+(60°-30°)=120°.
第二种情况,若逆时针旋转α度(60°≤α<90°),
据题意得90°-α=2(α-60°),
得α=70°,
∴∠EBC=90°-(70°-60°)=80°.
第三种情况:若顺时针旋转α度,如图3,
据题意得90°+α=2(60°+α),
得α=-30°,
∵0<α<90°,α=-30°不合题意,舍去,
故∠EBC=∠120°或80°.
点评 本题主要考查了角度的计算,正确认识三角板的角的度数,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.把多項式a2-4a分解因式,结果正确的是( )
| A. | a(a+2)(a-2) | B. | a(a-4) | C. | (a+2)(a-2) | D. | (a-2)2-4 |
17.小王上周五买进某种股票1000股,每股28元:如表为本周每天收盘时刻股票的涨跌情况:(单位:元)
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)若小王按本周五的收盘价将股票全部卖出,你认为他会获利吗?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +1 | +1.5 | -1.5 | -2.5 | +0.5 |
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)若小王按本周五的收盘价将股票全部卖出,你认为他会获利吗?
7.下列比较大小正确的是( )
| A. | -$\frac{3}{4}$>-$\frac{4}{3}$ | B. | -(-$\frac{1}{3}$)<-|-$\frac{1}{3}$| | C. | (-2)3<-23 | D. | (-3)2<(-2)3 |
11.9的平方根是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | ±9 |
12.点(-4,-2)关于y轴对称的点的坐标是( )
| A. | (4,-2) | B. | (-4,2) | C. | (-4,-2) | D. | (4,2) |
 如图,在⊙O中,AB是⊙O的直径,AB=8cm,C、D为弧AB的三等分点,M是AB上一动点,CM+DM的最小值是8cm.
如图,在⊙O中,AB是⊙O的直径,AB=8cm,C、D为弧AB的三等分点,M是AB上一动点,CM+DM的最小值是8cm.